题目内容
某商品在近30天内每件的销售价格p(元)与时间t(天)的函数关系是p=
,该商品的日销售量Q(件)与时间t(天)的函数关系是Q=-t+40(0<t≤30,t∈N),求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几天?
|
考点:分段函数的应用
专题:计算题,应用题,函数的性质及应用
分析:设日销售金额为y(元),则y=p•Q,对每段化简和配方,根据二次函数的性质,分别求解每段函数的最大值,由此能求出商品的日销售额y的最大值.
解答:
解:设日销售金额为y(元),则y=p•Q,
y=
=
=
,
当0<t<25,t∈N,t=10时,ymax=900(元);
当25≤t≤30,t∈N,t=25时,ymax=1125(元).
由1125>900,知ymax=1125(元),且第25天,日销售额最大.
y=
|
=
|
=
|
当0<t<25,t∈N,t=10时,ymax=900(元);
当25≤t≤30,t∈N,t=25时,ymax=1125(元).
由1125>900,知ymax=1125(元),且第25天,日销售额最大.
点评:本题考查分段函数在生产实际中的应用,考查二次函数的最值问题和运算求解能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,在△ABC中,
=2
,记
=
,
=
,则
=( )

| CD |
| DB |
| AB |
| a |
| AC |
| b |
| AD |

A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
若点(x,y)在映射f下的象为点(2x,x-y),则(-1,2)在映射f下的原象为( )
| A、(-2,-3) | ||||
| B、(-2,1) | ||||
C、(
| ||||
D、(-
|
 下列命题:
下列命题: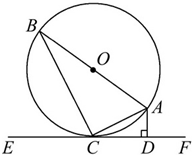 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.