题目内容
5.已知x>$\frac{1}{2}$,则函数f(x)=$\frac{1-2x}{{x}^{2}-2x+\frac{11}{4}}$的最小值是-$\frac{4\sqrt{2}+2}{7}$.分析 令2x-1=t(t>0),即x=$\frac{1}{2}$(t+1),即有函数即为$\frac{-4}{t+\frac{8}{t}-2}$,再由基本不等式和函数的单调性即可得到最小值.
解答 解:令2x-1=t(t>0),即x=$\frac{1}{2}$(t+1),
即有函数y=$\frac{-t}{\frac{1}{4}(t+1)^{2}-(t+1)+\frac{11}{4}}$=$\frac{-4}{t+\frac{8}{t}-2}$,
由t+$\frac{8}{t}$≥2$\sqrt{t•\frac{8}{t}}$=4$\sqrt{2}$,
当且仅当t=2$\sqrt{2}$,即x=$\sqrt{2}$+$\frac{1}{2}$时,取得等号.
即有函数f(x)≥$\frac{-4}{4\sqrt{2}-2}$=-$\frac{4\sqrt{2}+2}{7}$.
故f(x)的最小值为-$\frac{4\sqrt{2}+2}{7}$.
故答案为:-$\frac{4\sqrt{2}+2}{7}$.
点评 本题考查函数的最值的求法,注意运用换元法和基本不等式,应注意满足的条件:一正二定三等,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
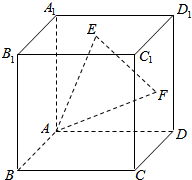 如图,在正方体ABCD-A1B1C1D1中,E、F分别为A1B1C1D1,CDD1C1的中心,试用向量$\overrightarrow{{B}_{1}B}$,$\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{{B}_{1}{A}_{1}}$表示向量:
如图,在正方体ABCD-A1B1C1D1中,E、F分别为A1B1C1D1,CDD1C1的中心,试用向量$\overrightarrow{{B}_{1}B}$,$\overrightarrow{{B}_{1}{C}_{1}}$,$\overrightarrow{{B}_{1}{A}_{1}}$表示向量: