题目内容
13.某地要建造一个水库,设计中,水库的最大容水量为12800立方米,山洪暴发时,预测注入水库的水量Sn(立方米)与天数n(n∈N+,n≤10)的关系是Sn=5000$\sqrt{n(n+24)}$,此水库原有水量为80000立方米,泄水闸每天的泄水量为4000立方米,若山洪暴发的第一天就打开泄水闸.(1)写出第n天水库的水量f(n)与天数n之间的函数关系式;
(2)在这10天中,堤坝会发生危险吗?(水库的水量不小于它的最大容水量,堤坝就会发生危险)
分析 (1)根据条件求出注水量和泄水量,即可得到结论.
(2)根据堤坝会发生危险的条件,解不等式即可.
解答 解:(1)设第n天注入水库的水量为5000$\sqrt{n(n+24)}$立方米,泄水为4000n立方米,
则第n天水库的容水量为f(n)=8000+5000$\sqrt{n(n+24)}$-4000n,(n∈N+,n≤10).
(2)设第n天会发生危险,则
5000$\sqrt{n(n+24)}$-4000n≥128000-80000,
即5$\sqrt{n(n+24)}$≥4n+48,
也即n2+24n-256≥0,
解得n≤-32或n≥8,
由于n∈N,所以取n≥8,即第8天时,总水量就超过水库的最大容量,也即该水库堤坝在第8天会发生危险.
点评 本题主要考查函数的应用问题,根据条件建立函数关系是解决本题的关键.

练习册系列答案
相关题目
3.函数y=$\frac{2}{x}$的单调减区间为( )
| A. | R | B. | (-∞,0)∪(0,+∞) | C. | (-∞,0),(0,+∞) | D. | (0,+∞) |
4.设函数f(x)是奇函数,并且在R上为增函数,若0≤θ≤$\frac{π}{6}$时,f(msinθ)+f(1-m)>0恒成立,则实数m的取值范围是( )
| A. | (0,1) | B. | (0,$\frac{1}{2}$) | C. | (-∞,2) | D. | (-∞,1) |
18.设sinθ=$\frac{3}{5}$,cosθ=-$\frac{4}{5}$,则2θ的终边所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.设f(x)=(x-1)3+x+2,{an}是公差为$\frac{1}{2}$的等差数列,且f(a1)+f(a2)+f(a3)+f(a4)+f(a5)+f(a6)=18,则a1=( )
| A. | -$\frac{1}{4}$ | B. | -$\frac{7}{4}$ | C. | -$\frac{5}{4}$ | D. | -$\frac{3}{4}$ |
3.已知A,B,C是△ABC的三个内角,且满足2sinA=$\sqrt{3}$sinC-sinB,则角A的取值范围为( )
| A. | (0,$\frac{π}{6}$] | B. | (0,$\frac{π}{3}$] | C. | (0,$\frac{π}{2}$] | D. | [$\frac{π}{3}$,$\frac{2π}{3}$] |
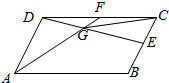 如图,已知E,F分别是平行四边形ABCD的边BC,CD中点,AF与DE相交于点G,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{GC}$=$\frac{3}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示)
如图,已知E,F分别是平行四边形ABCD的边BC,CD中点,AF与DE相交于点G,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,则$\overrightarrow{GC}$=$\frac{3}{5}\overrightarrow{a}+\frac{1}{5}\overrightarrow{b}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示)