题目内容
已知数列{
}是公差为2的等差数列,且a1=1.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{anan+1}的前n项和为Tn.证明:
≤Tn<
.
| 1 |
| an |
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{anan+1}的前n项和为Tn.证明:
| 1 |
| 3 |
| 1 |
| 2 |
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)利用等差数列的通项公式,求出数列{an}的通项公式;
(Ⅱ)利用裂项求出和,求出Tn,由n∈N+和Tn单调性可求出Tn的取值范围.
(Ⅱ)利用裂项求出和,求出Tn,由n∈N+和Tn单调性可求出Tn的取值范围.
解答:
解:(Ⅰ)由已知列{
}为公差为2的等差数列,
∴
=
+(n-1)•2,又a1=1,∴
=2n-1,
∴an=
;
(Ⅱ)由(Ⅰ)知anan+1=
•
=
(
-
),
∴Tn=a1a2+a2a3+…anan+1
=
(1-
+
-
+…+
-
)=
,
∴Tn=
-
<
,又∵Tn=
=
,Tn随n的增大而增大,
∴Tn≥T1=
,
∴
≤Tn<
.
| 1 |
| an |
∴
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| an |
∴an=
| 1 |
| 2n-1 |
(Ⅱ)由(Ⅰ)知anan+1=
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=a1a2+a2a3+…anan+1
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 2(2n+1) |
| 1 |
| 2 |
| n |
| 2n+1 |
| 1 | ||
2+
|
∴Tn≥T1=
| 1 |
| 3 |
∴
| 1 |
| 3 |
| 1 |
| 2 |
点评:本题考查等差数列的通项公式和裂项求和,还考查了函数的单调性,裂项求和是最重要的数列求和方法这一.属于中档题.

练习册系列答案
相关题目
已知i为虚数单位.z为复数,下面叙述正确的是( )
A、z-
| ||
| B、任何数的偶数次幂均为非负数 | ||
| C、i+1的共轭复数为i-l | ||
| D、2+3i的虚部为3 |
已知数列{an},a1=
,an=1-
(n≥2),则a2014=( )
| 1 |
| 4 |
| 1 |
| an-1 |
A、
| ||
B、
| ||
| C、-3 | ||
D、
|
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|≤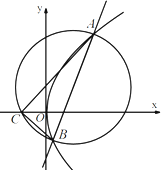 已知抛物线的顶点为(0,0),准线为x=-2,不垂直于x轴的直线x=ty+1与该抛物线交于A,B两点,圆M以AB为直径.
已知抛物线的顶点为(0,0),准线为x=-2,不垂直于x轴的直线x=ty+1与该抛物线交于A,B两点,圆M以AB为直径.