题目内容

若曲线f（x）=ax2-lnx存在垂直于y轴的切线，则实数a的取值范围是
 
．
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：由曲线f（x）=ax2-lnx存在垂直于y轴的切线，故f′（x）=0有实数解，运用参数分离，根据函数的定义域即可解出a的取值范围．
解答： 解：∵曲线f（x）=ax2-lnx存在垂直于y轴的切线，（x＞0）
∴f′（x）=2ax-
1
x
=0有解，即得a=
1
2x2
有解，
∵x＞0，∴
1
2x2
＞0，即a＞0．
∴实数a的取值范围是a＞0．
故答案为：a＞0．
点评：本题主要考查了利用导数研究曲线上某点切线方程，函数零点等有关基础知识，考查运算求解能力、推理论证能力，考查化归与转化思想．
练习册系列答案
相关题目
某市规定，高中学生三年在校期间参加不少于80小时的社区服务才合格．教育部门在全市随机抽取200学生参加社区服务的数据，按时间段[75，80），[80，85），[85，90），[90，95），[95，100]（单位：小时）进行统计，其频率分布直方图如图所示．

（Ⅰ）求抽取的200位学生中，参加社区服务时间不少于90小时的学生人数，并估计从全市高中学生中任意选取一人，其参加社区服务时间不少于90小时的概率；
（Ⅱ）从全市高中学生（人数很多）中任意选取3位学生，记ξ为3位学生中参加社区服务时间不少于90小时的人数．试求随机变量ξ的分布列和数学期望Eξ．
若S1=
∫
3
2
1
x
dx，S2=
∫
π
0
cos
x
2
dx，则S1、S2的大小关系为
 
．
农业技术员进行某种作物的种植密度试验，把一块试验田划分为8块面积相等的区域（除了种植密度，其它影响作物生长的因素都保持一致），种植密度和单株产量统计如下：

根据上表所提供信息，第
 
号区域的总产量最大，该区域种植密度为
 
株/m2．
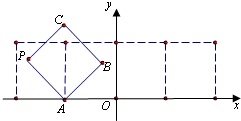如图放置的边长为1的正方形PABC沿x轴滚动，点B恰好经过原点．设顶点P（x，y）的轨迹方程是y=f（x），则对函数y=f（x）有下列判断：
①函数y=f（x）是偶函数；
②对任意的x∈R，都有f（x+2）=f（x-2）；
③函数y=f（x）在区间[2，3]上单调递减；
④
∫
2
0
f（x）dx=
π+1
2
．
其中判断正确的序号是
 
．
当圆x2+y2=4的圆心到直线y=kx+1的距离最大时，k=
 
．
过点（2，-1）引直线与抛物线y=x2只有一个公共点，这样的直线共有
 
条．
设定义在R上的函数f（x）满足f（1）=1，f′（x）＞
1
3
，其中f′（x）是f（x）的导函数，则不等式
f（x3）＜
1
3
x3+
2
3
的解集为
 
．
下列函数中，既是偶函数又在（-∞，0）上单调递增的是（　　）
A、y=x2
B、y=2|x|
C、y=log2
1
|x|
D、y=sinx

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网