Question

如图是某校校门的一个局部的截面设计图，CA=AO=OB=2米，

EF

是以O为圆心、OA为半径的圆的一段弧（E、F两点分别在OC、OD上），∠AOC=∠BOD=θ（θ≤

π

4

），OD=k•OC（k是常数且1＜k≤3）．通过对材料性能进行测算，“跨度比”

CD

OC

不能超过

3k+1

． 
（1）将该截面（图中实线围成的区域）的面积S表示为θ的函数；
（2）为使该门口显得相对大气，截面积S越大越好． 当S最大时，试求cosθ的值．

Answer 1

考点：余弦定理,解三角形的实际应用

专题：导数的综合应用,三角函数的求值

分析：（1）根据平角的定义得到∠COD=π-2θ，再由OD=k•OC，CD≤

3k+1

•OC，利用余弦定理列出不等式，求出cos2θ的范围，利用三角形面积公式表示出S与θ的关系式即可；
（2）利用求导法则求出S′，令S′=0表示出cos2θ的值，分两种情况考虑：①若

1

1+k

≤

3-k

2

；②若

1

1+k

＞

3-k

2

，分别求出S最大时，cosθ的值即可．

解答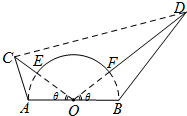： 解：（1）易知∠COD=π-2θ，由OD=k•OC，CD≤

3k+1

•OC，
根据余弦定理得：CD²=OC²+（k•OC）²-2•OC•（k•OC）cos（π-2θ）≤（

3k+1

•OC）²，
整理得：cos2θ≤

3-k

2

，记满足cos2θ=

3-k

2

的锐角θ为θ₀，
∵S_△AOC=

1

2

•OA•ACsin（π-2θ）=2sin2θ，
∴S=S_△AOC+S_△BOD+S_扇形EOF=（1+k）S_△AOC+S_扇形EOF=2（1+k）sin2θ+

1

2

•（π-2θ）•2²=2（1+k）sin2θ-4θ+2π，
∴S=2（1+k）sin2θ-4θ+2π（θ₀≤θ≤

π

4

）；
（2）由S=2（1+k）sin2θ-4θ+2π，得S′=4（1+k）cos2θ-4，
令S′=0，得cos2θ=

1

1+k

，
①若

1

1+k

≤

3-k

2

，即1＜k≤1+

2

，则cos2θ=

1

1+k

时，S取得最大值，
此时cosθ=

1+cos2θ 2

=

k+2 2(k+1)

；
②若

1

1+k

＞

3-k

2

，即1+

2

＜k≤3，则cos2θ=

3-k

2

时，S取得最大值，
此时cosθ=

1+cos2θ 2

=

5-k

2

．

点评：此题考查了余弦定理，利用导数研究函数的增减性，以及三角形的面积公式，熟练掌握定理是解本题的关键．