题目内容
设M为抛物线C:x2=4py(p>0)准线上的任意一点,过点M作曲线C的两条切线,设切点为A、B.
(Ⅰ)直线AB是否过定点?如果是,求出该定点,如果不是,请说明理由;
(Ⅱ)当直线MA,MF,MB的斜率均存在时,求证:直线MA,MF,MB的斜率的倒数成等差数列.
(Ⅰ)直线AB是否过定点?如果是,求出该定点,如果不是,请说明理由;
(Ⅱ)当直线MA,MF,MB的斜率均存在时,求证:直线MA,MF,MB的斜率的倒数成等差数列.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设M(m,-p),两切点为A(x1,y1),B(x2,y2),由x2=2py,得y=
x2,求导得两条切线方程为y-y1=
x1(x-x1),y-y2=
x2(x-x2),从而求出x1,x2为方程x2-2mx-4p2=0的两根,由此能求出直线恒过定点(0,p).
(Ⅱ)设M(m,-p),A(x1,y1),B(x2,y2),x1+x2=2m,x1x2=-4p2,由此能证明直线MA,MF,MB的斜率倒数成等差数列.
| 1 |
| 4p |
| 1 |
| 2p |
| 1 |
| 2p |
(Ⅱ)设M(m,-p),A(x1,y1),B(x2,y2),x1+x2=2m,x1x2=-4p2,由此能证明直线MA,MF,MB的斜率倒数成等差数列.
解答:
(Ⅰ)解:设M(m,-p),两切点为A(x1,y1),B(x2,y2),
由x2=2py,得y=
x2,求导得y′=
x.
∴两条切线方程为y-y1=
x1(x-x1),①
y-y2=
x2(x-x2),②…2分
对于方程①,代入点M(m,-p)得,-p-y1=
x1(m-x1),
又y1=
x12,
∴-p-
x12=
x1(m-x1),
整理得:x12-2mx1-4p2=0,
同理对方程②有x22-2mx2-4p2=0,
即x1,x2为方程x2-2mx-4p2=0的两根.
∴x1+x2=2m,x1x2=-4p2,③…4分
设直线AB的斜率为k,k=
=
=
(x1+x2),
∴直线AB的方程为y-
=
(x1+x2)(x-x1),
展开得:y=
(x1+x2)x-
,
代入③得:y=
x+p,∴直线恒过定点(0,p).…6分
(Ⅱ)证明:由(Ⅰ)的结论,设M(m,-p),A(x1,y1),B(x2,y2),
且有x1+x2=2m,x1x2=-4p2,
∴kMA=
,kMB=
,
∴
+
=
+
=
+
=
+
=
+
=
=
=
=-
,
又∵
=
=-
,
∴
+
=
.
即直线MA,MF,MB的斜率倒数成等差数列.…13分
由x2=2py,得y=
| 1 |
| 4p |
| 1 |
| 2p |
∴两条切线方程为y-y1=
| 1 |
| 2p |
y-y2=
| 1 |
| 2p |
对于方程①,代入点M(m,-p)得,-p-y1=
| 1 |
| 2p |
又y1=
| 1 |
| 4p |
∴-p-
| 1 |
| 4p |
| 1 |
| 2p |
整理得:x12-2mx1-4p2=0,
同理对方程②有x22-2mx2-4p2=0,
即x1,x2为方程x2-2mx-4p2=0的两根.
∴x1+x2=2m,x1x2=-4p2,③…4分
设直线AB的斜率为k,k=
| y2-y1 |
| x2-x1 |
| x22-x12 |
| 4p(x2-x1) |
| 1 |
| 4p |
∴直线AB的方程为y-
| x12 |
| 4p |
| 1 |
| 4p |
展开得:y=
| 1 |
| 4p |
| x1x2 |
| 4p |
代入③得:y=
| m |
| 2p |
(Ⅱ)证明:由(Ⅰ)的结论,设M(m,-p),A(x1,y1),B(x2,y2),
且有x1+x2=2m,x1x2=-4p2,
∴kMA=
| y1+p |
| x1-m |
| y2+p |
| x2-m |
∴
| 1 |
| kMA |
| 1 |
| kMB |
| x1-m |
| y1+p |
| x2-m |
| y2+p |
=
| x1-m | ||
|
| x2-m | ||
|
=
| 4p(x1-m) |
| x12+4p2 |
| 4p(x2-m) |
| x22+4p2 |
=
| 4p(x1-m) |
| x12-x1x2 |
| 4p(x2-m) |
| x22-x1 x2 |
=
| 4p(x1-m)x2-4p(x2-m)x1 |
| x1 x2(x1-x2) |
=
| 4pm |
| x1x2 |
| 4pm |
| -4p2 |
| m |
| p |
又∵
| 1 |
| kMP |
| m |
| -p-p |
| m |
| 2p |
∴
| 1 |
| kMA |
| 1 |
| kMB |
| 2 |
| kMP |
即直线MA,MF,MB的斜率倒数成等差数列.…13分
点评:本题考查直线是否恒过定点的判断,考查三条直线的斜率倒数成等差数列的证明,考查圆锥曲线切线,直线过定点,圆锥曲线计算能力等,是难题.

练习册系列答案
相关题目
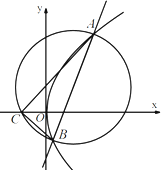 已知抛物线的顶点为(0,0),准线为x=-2,不垂直于x轴的直线x=ty+1与该抛物线交于A,B两点,圆M以AB为直径.
已知抛物线的顶点为(0,0),准线为x=-2,不垂直于x轴的直线x=ty+1与该抛物线交于A,B两点,圆M以AB为直径. 
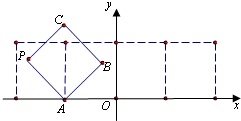 如图放置的边长为1的正方形PABC沿x轴滚动,点B恰好经过原点.设顶点P(x,y)的轨迹方程是y=f(x),则对函数y=f(x)有下列判断:
如图放置的边长为1的正方形PABC沿x轴滚动,点B恰好经过原点.设顶点P(x,y)的轨迹方程是y=f(x),则对函数y=f(x)有下列判断: