题目内容
 已知直角梯形ABCD中,AD∥BC,AD=AB=
已知直角梯形ABCD中,AD∥BC,AD=AB=| 1 |
| 2 |
(1)求证:BD⊥DC;
(2)求三棱锥P-BCD的体积.
考点:棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:(1)由已知得∠ADB=∠DBC=45°,过D作DM⊥BC,垂足为M,则DM=AB=MC=2,从而∠BDC=90°,由此能证明BD⊥DC.
(2)取AB中点O,连结PO,由已知得PO⊥平面ABCD,S△BCD=S梯形ABCD-S△ABD,由此能求出VP-BCD.
(2)取AB中点O,连结PO,由已知得PO⊥平面ABCD,S△BCD=S梯形ABCD-S△ABD,由此能求出VP-BCD.
解答:
(1)证明:∵AD=2,AB=2,AD⊥AB,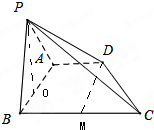
∴∠ADB=∠DBC=45°,
过D作DM⊥BC,垂足为M,则DM=AB=MC=2,
∴∠DCM=45°,∴∠BDC=90°,∴BD⊥DC.…(6分)
(2)解:取AB中点O,连结PO,
∵△PAB是等边三角形,平面PAB⊥平面ABCD,
∴PO⊥平面ABCD,
∵AD=AB=
BC=2,∴PO=
=
,
∵S△BCD=S梯形ABCD-S△ABD=
(2+4)×2-
×2×2=4,
∴VP-BCD=
×PO×S△BCD=
×
×4=
.…(12分)

∴∠ADB=∠DBC=45°,
过D作DM⊥BC,垂足为M,则DM=AB=MC=2,
∴∠DCM=45°,∴∠BDC=90°,∴BD⊥DC.…(6分)
(2)解:取AB中点O,连结PO,
∵△PAB是等边三角形,平面PAB⊥平面ABCD,
∴PO⊥平面ABCD,
∵AD=AB=
| 1 |
| 2 |
| 22-12 |
| 3 |
∵S△BCD=S梯形ABCD-S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∴VP-BCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
点评:本题考查异面直线垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要注意空间中线线、线面、面面间的位置关系及性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
常用以下方法求函数y=[f(x)]g(x)的导数:先两边同取以e为底的对数(e≈2.71828…,为自然对数的底数)得lny=g(x)lnf(x),再两边同时求导,得
•y′=g′(x)lnf(x)+g(x)•[lnf(x)]′,即y′=[f(x)]g(x){g′(x)lnf(x)+g(x)•[lnf(x)]′}.运用此方法可以求函数h(x)=xx(x>0)的导函数.据此可以判断下列各函数值中最小的是( )
| 1 |
| y |
A、h(
| ||
B、h(
| ||
C、h(
| ||
D、h(
|
设全集I=R,集合A={y|y=log2x,x>2},B={x|y=
},则( )
| x-1 |
| A、A⊆B |
| B、A∪B=A |
| C、A∩B=∅ |
| D、A∩(∁IB)≠∅ |
(已知集合A={x||x+1|<1},B{x|y=
},则A∩B=( )
| 1 | ||
|
| A、(-2,-1) |
| B、(-2,-1] |
| C、(-1,0) |
| D、[-1,0) |
设非零向量
,
,则“
,
的夹角为锐角”是“|
+
|>|
-
|”的( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
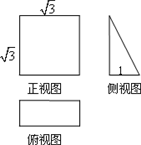 一个空间几何体的三视图及部分数据如图所示,则这个几何体的体积为( )
一个空间几何体的三视图及部分数据如图所示,则这个几何体的体积为( )A、
| ||
| B、1 | ||
C、
| ||
| D、3 |
某组合体的三视图如图所示,其中俯视图的扇形中心角为60°,则该几何体的体积为( )


A、
| ||||
B、
| ||||
C、3
| ||||
D、3
|