题目内容
已知|
|=4，|
|=8，
与
的夹角是60°
（1）计算|
+
|；
（2）当k为何值时，（
+2
）⊥（k
-
）．
| a |
| b |
| a |
| b |
（1）计算|
| a |
| b |
（2）当k为何值时，（
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：（1）运用向量的数量积的定义和向量的模的平方即为斜率的平方，计算即可得到；
（2）运用向量垂直的条件：数量积为0，化简整理，解方程即可得到k．
（2）运用向量垂直的条件：数量积为0，化简整理，解方程即可得到k．
解答：
解：（1）由|
|=4，|
|=8，
与
的夹角是60°，
则
•
=4×8×cos60°=16，
|
+
|=
=
=
=4
；
（2）由（
+2
）⊥（k
-
），
则（
+2
）•（k
-
）=0，
即k
2-2
2+（2k-1）
•
=0，
即有16k-128+16（2k-1）=0，
解得k=3．
即有当k为3时，（
+2
）⊥（k
-
）．
| a |
| b |
| a |
| b |
则
| a |
| b |
|
| a |
| b |
(
|
|
| 16+64+16 |
=4
| 6 |
（2）由（
| a |
| b |
| a |
| b |
则（
| a |
| b |
| a |
| b |
即k
| a |
| b |
| a |
| b |
即有16k-128+16（2k-1）=0，
解得k=3．
即有当k为3时，（
| a |
| b |
| a |
| b |
点评：本题考查向量的数量积的定义和性质，主要考查向量垂直的条件：数量积为0，向量的平方即为模的平方，考查运算能力，属于基础题．
练习册系列答案
全程金卷系列答案
相关题目
复数
（i是虚数单位）的虚部是（ ）
| 1 |
| i-1 |
| A、1 | ||
| B、i | ||
C、-
| ||
D、
|
已知直角梯形ABCD中，AD∥BC，AD=AB=函数f（x）=log2（x-1）的零点是（ ）
| A、（1，0） | B、（2，0） |
| C、1 | D、2 |
如图，在四棱锥S-ABCD中，底面ABCD是边长为a的正方形，SA=a且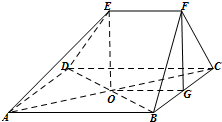
如图，在多面体ABCDEF中，四边形ABCD是菱形，AC，BD相交于点O，EF∥AB，AB=2EF，平面BCF⊥平面ABCD，BF=CF，点G为BC的中点．