题目内容
常用以下方法求函数y=[f(x)]g(x)的导数:先两边同取以e为底的对数(e≈2.71828…,为自然对数的底数)得lny=g(x)lnf(x),再两边同时求导,得
•y′=g′(x)lnf(x)+g(x)•[lnf(x)]′,即y′=[f(x)]g(x){g′(x)lnf(x)+g(x)•[lnf(x)]′}.运用此方法可以求函数h(x)=xx(x>0)的导函数.据此可以判断下列各函数值中最小的是( )
| 1 |
| y |
A、h(
| ||
B、h(
| ||
C、h(
| ||
D、h(
|
考点:导数的运算
专题:导数的概念及应用
分析:根据定义,先求原函数的导数,分别令导数大于0,小于0,解不等式求出函数的单调区间,从而求出函数的最小值.
解答:
解:(h(x))′=xx[x′lnx+x(lnx)′]
=xx(lnx+1),
令h(x)′>0,解得:x>
,令h(x)′<0,解得:0<x<
,
∴h(x)在(0,
)递减,在(
,+∞)递增,
∴h(
)最小,
故选:B.
=xx(lnx+1),
令h(x)′>0,解得:x>
| 1 |
| e |
| 1 |
| e |
∴h(x)在(0,
| 1 |
| e |
| 1 |
| e |
∴h(
| 1 |
| e |
故选:B.
点评:本题考查函数的导数的应用,极值的求法,基本知识的考查.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
复数
(i是虚数单位)的虚部是( )
| 1 |
| i-1 |
| A、1 | ||
| B、i | ||
C、-
| ||
D、
|
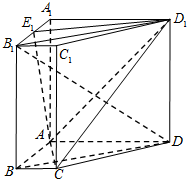 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=1,AB=
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,BC=1,AB= 已知直角梯形ABCD中,AD∥BC,AD=AB=
已知直角梯形ABCD中,AD∥BC,AD=AB=