题目内容
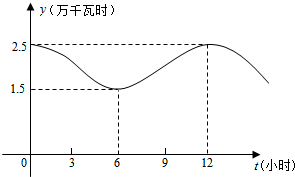 某大型企业一天中不同时刻的用电量y(单位:万千瓦时)关于时间t(0≤t≤24,单位:小时)的函数y=f(t)近似地满足f(t)=Asin(ωt+φ)+B(A>0,ω>0,0<φ<π),如图是该企业一天中在0点至12点时间段用电量y与时间t的大致图象.
某大型企业一天中不同时刻的用电量y(单位:万千瓦时)关于时间t(0≤t≤24,单位:小时)的函数y=f(t)近似地满足f(t)=Asin(ωt+φ)+B(A>0,ω>0,0<φ<π),如图是该企业一天中在0点至12点时间段用电量y与时间t的大致图象.(Ⅰ)根据图象,求A,ω,φ,B的值;
(Ⅱ)若某日的供电量g(t)(万千瓦时)与时间t(小时)近似满足函数关系式g(t)=-15t+20(0≤t≤12).当该日内供电量小于该企业的用电量时,企业就必须停产.请用二分法计算该企业当日停产的大致时刻(精确度0.1).
参考数据:
| t(时) | 10 | 11 | 12 | 11.5 | 11.25 | 11.75 | 11.625 | 11.6875 |
| f(t)(万千瓦时) | 2.25 | 2.433 | 2.5 | 2.48 | 2.462 | 2.496 | 2.490 | 2.493 |
| g(t)(万千瓦时) | 5 | 3.5 | 2 | 2.75 | 3.125 | 2.375 | 2.563 | 2.469 |
考点:在实际问题中建立三角函数模型
专题:三角函数的图像与性质
分析:(Ⅰ)根据图象可分别求得函数的周期,A,B,求得ω,把已知点(0,25)代入求得φ,则函数的解析式可得.
(Ⅱ)令h(9t)=f(t)-g(t),根据图表,确定h(t)接近于0时t的值.
(Ⅱ)令h(9t)=f(t)-g(t),根据图表,确定h(t)接近于0时t的值.
解答:
解:(Ⅰ)由图知T=12,ω=
,
A=
=
,B=
=2.
∴y=
sin(
x+φ)+2.
又函数过点(0,25).
代入,得φ=
+2kπ,又0<φ<π,
∴φ=
.
综上,A=
,ω=
,φ=
,B=
.
即f(t)=
sin(
t+
)+2.
(Ⅱ)令h(t)=f(t)-g(t),设h(t0)=0,则t0为该企业的停产时间.
由h(11)=f(11)-g(11)<0,h(12)=f(12)-g(12)>0,则t0∈(11,12).
又h(11.5)=f(11.5)-g(11.5)<0,则t0∈(11.5,12).
又h(11.75)=f(11.5)-g(11.75)>0,则t0∈(11.5,11.75).
又h(11.625)=f(11.625)-g(11.625)<0,则t0∈(11.625,11.75).
又h(11.6875)=f(11.6875)-g(11.6875)>0,则t0∈(11.625,11.6875).
∵|11.6875-11.625|=0.0625<0.1.
∴应该在11.625时停产.
| π |
| 6 |
A=
| ymax-ymin |
| 2 |
| 1 |
| 2 |
| ymax+ymin |
| 2 |
∴y=
| 1 |
| 2 |
| π |
| 6 |
又函数过点(0,25).
代入,得φ=
| π |
| 2 |
∴φ=
| π |
| 2 |
综上,A=
| 1 |
| 2 |
| π |
| 6 |
| π |
| 2 |
| 1 |
| 2 |
即f(t)=
| 1 |
| 2 |
| π |
| 6 |
| π |
| 2 |
(Ⅱ)令h(t)=f(t)-g(t),设h(t0)=0,则t0为该企业的停产时间.
由h(11)=f(11)-g(11)<0,h(12)=f(12)-g(12)>0,则t0∈(11,12).
又h(11.5)=f(11.5)-g(11.5)<0,则t0∈(11.5,12).
又h(11.75)=f(11.5)-g(11.75)>0,则t0∈(11.5,11.75).
又h(11.625)=f(11.625)-g(11.625)<0,则t0∈(11.625,11.75).
又h(11.6875)=f(11.6875)-g(11.6875)>0,则t0∈(11.625,11.6875).
∵|11.6875-11.625|=0.0625<0.1.
∴应该在11.625时停产.
点评:本题主要考查了三角函数图象 与性质解决实际问题.解题过程中确定函数的解析式是解决问题的前提.

练习册系列答案
相关题目
在(1+x)6(1+y)4的展开式中,记xmyn项的系数为f(m,n),则f(2,1)+f(1,2)=( )
| A、45 | B、60 | C、96 | D、108 |
设函数f(x)=
,g(x)=x2f(x-1),则函数g(x)的递减区间是( )
|
| A、(0,1] |
| B、(0,1) |
| C、(-∞,0) |
| D、(0,+∞) |
已知集合A={x|log4x<1},集合B={x|2x<8},则A∩B等于( )
| A、(-∞,4) |
| B、(0,4) |
| C、(0,3) |
| D、(-∞,3) |
