题目内容
如图所示，已知几何体的三视图，则该几何体的表面积为 ，体积为 ．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由三棱柱的三视图可得该几何体是一个圆锥，求出底面半径，圆锥的高，及母线长，代入圆锥体积和表面积公式，可得答案．
解答：
解：由三棱柱的三视图可得该几何体是一个圆锥，
底面直径为2cm，故底面半径r=1cm，
圆锥的高h=2cm，
故圆锥的母线l=
=
cm，
故圆锥的表面积S=πrl=
πcm2，
圆锥的体积V=
πr2h=
πcm3，
故答案为：
πcm2，
πcm3
底面直径为2cm，故底面半径r=1cm，
圆锥的高h=2cm，
故圆锥的母线l=
| 22-12 |
| 3 |
故圆锥的表面积S=πrl=
| 3 |
圆锥的体积V=
| 1 |
| 3 |
| 2 |
| 3 |
故答案为：
| 3 |
| 2 |
| 3 |
点评：本题考查了由三视图求原几何体的体积和表面积，解答的关键是由三视图还原原图形，是基础的计算题．
练习册系列答案
全能测控一本好卷系列答案
相关题目
已知圆x2+y2+mx-
=0与抛物线y2=4x的准线相切，则m=（ ）
| 1 |
| 4 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
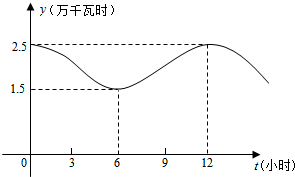某大型企业一天中不同时刻的用电量y（单位：万千瓦时）关于时间t（0≤t≤24，单位：小时）的函数y=f（t）近似地满足f（t）=Asin（ωt+φ）+B（A＞0，ω＞0，0＜φ＜π），如图是该企业一天中在0点至12点时间段用电量y与时间t的大致图象．已知四个数：①y=x．sinx②y=x．cosx③y=x．|cosx|④y=x•2x的图象如下，但顺序被打乱．则按照图象从左到右的顺序，对应的函数序号正确一组的是（ ）
| A、①④②③ | B、①④③② |
| C、④①②③③④②① |