题目内容
在（1+x）6（1+y）4的展开式中，记xmyn项的系数为f（m，n），则f（2，1）+f（1，2）=（ ）
| A、45 | B、60 | C、96 | D、108 |
考点：二项式系数的性质
专题：二项式定理
分析：按照二项式定理把（1+x）6（1+y）4展开，求得f（2，1）和f（1，2）的值，可得f（2，1）+f（1，2）的值．
解答：
解：（1+x）6（1+y）4 =（1+6x+15x2+20x3+15x4+6x5+x6） （1+4y+6y2+4y3+y4），
∴f（2，1）=15×4=60，f（1，2）=6×6=36，∴f（2，1）+f（1，2）=96，
故选：C．
∴f（2，1）=15×4=60，f（1，2）=6×6=36，∴f（2，1）+f（1，2）=96，
故选：C．
点评：本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
如图，一小山峰BC的高为30cm，山顶上有建筑物CD的高为20cm，建筑物上竖一高为40m铁架DE，问在底面上距离B多远的地方，能找到这样一点A，使得∠BAC=∠DAE？
如图，在棱长为2的正方体ABCD-A1B1C1D1中，E为DD1的中点
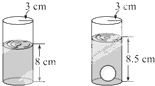一个圆柱形的玻璃瓶的内半径为3cm，瓶里所装的水深为8cm，将一个钢球完全浸入水中，瓶中水的高度上升到8.5cm，则钢球的半径为（ ）| A、1 cm |
| B、1.2 cm |
| C、1.5 cm |
| D、2 cm |
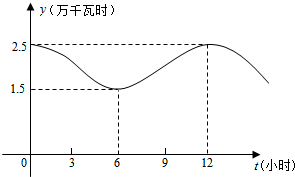某大型企业一天中不同时刻的用电量y（单位：万千瓦时）关于时间t（0≤t≤24，单位：小时）的函数y=f（t）近似地满足f（t）=Asin（ωt+φ）+B（A＞0，ω＞0，0＜φ＜π），如图是该企业一天中在0点至12点时间段用电量y与时间t的大致图象．