题目内容
已知集合A={x|log4x<1},集合B={x|2x<8},则A∩B等于( )
| A、(-∞,4) |
| B、(0,4) |
| C、(0,3) |
| D、(-∞,3) |
考点:对数函数的单调性与特殊点,交集及其运算
专题:计算题,函数的性质及应用,集合
分析:首先化简集合A,B,再求其交集.
解答:
解:A={x|log4x<1}=(0,4),
集合B={x|2x<8}=(-∞,3),
故A∩B=(0,3);
故选C.
集合B={x|2x<8}=(-∞,3),
故A∩B=(0,3);
故选C.
点评:本题考查了集合的化简与运算,属于基础题.

练习册系列答案
相关题目
近期由于某些原因,国内进口豪华轿车纷纷降价,某豪车原价为200万元,连续两次降价a%后,售价为148万元,则下面所列方程正确的是( )
| A、200(1+a%)2=148 |
| B、200(1-a%)2=148 |
| C、200(1-2a%)=148 |
| D、200(1-a%)=148 |
已知四个数:①y=x.sinx②y=x.cosx③y=x.|cosx|④y=x•2x的图象如下,但顺序被打乱.则按照图象从左到右的顺序,对应的函数序号正确一组的是( )

| A、①④②③ | B、①④③② |
| C、④①②③③④②① |
已知函数f(x)=|2x-2|,若m≠n,且f(m)=f(n),则m+n的取值范围是( )
| A、(1,+∞) |
| B、(2,+∞) |
| C、(-∞,1) |
| D、(-∞,2) |
设函数f(x)是偶函数,且当x>0时,f(x)=
,则在区间[-4,-2]内,函数f(x)( )
| 2 |
| x+1 |
A、单调递增,最大值
| ||
B、单调递减,最大值
| ||
C、单调递增,最小值
| ||
D、单调递增,最大值
|
若a<0,点p(-a2-1,-a+3)关于原点的对称点为p1,则p1在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知sinα•cosα=
,且
<α<
,则cosα-sinα=( )
| 1 |
| 8 |
| π |
| 4 |
| π |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
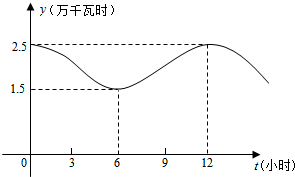 某大型企业一天中不同时刻的用电量y(单位:万千瓦时)关于时间t(0≤t≤24,单位:小时)的函数y=f(t)近似地满足f(t)=Asin(ωt+φ)+B(A>0,ω>0,0<φ<π),如图是该企业一天中在0点至12点时间段用电量y与时间t的大致图象.
某大型企业一天中不同时刻的用电量y(单位:万千瓦时)关于时间t(0≤t≤24,单位:小时)的函数y=f(t)近似地满足f(t)=Asin(ωt+φ)+B(A>0,ω>0,0<φ<π),如图是该企业一天中在0点至12点时间段用电量y与时间t的大致图象.