题目内容
把正方形ABCD沿对角线BD折成直二面角后,有如下四个结论:
①AC⊥BD; ②△ACD是等边三角形;
③AB与平面BCD成60°角; ④AB与CD所成角为60°
其中正确的结论是 .
①AC⊥BD; ②△ACD是等边三角形;
③AB与平面BCD成60°角; ④AB与CD所成角为60°
其中正确的结论是
考点:命题的真假判断与应用
专题:空间角,简易逻辑
分析:取BD的中点E,则AE⊥BD,CE⊥BD.根据线面垂直的判定及性质可判断①的真假;求出AC长后,可以判断②的真假;求出AB与平面BCD所成的角可判断③的真假;建立空间坐标系,利用向量法,求出AB与CD所成的角,可以判断④的真假;进而得到答案.
解答:
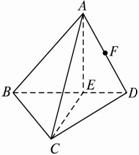 解:取BD的中点E,则AE⊥BD,CE⊥BD.?∴BD⊥面AEC.?
解:取BD的中点E,则AE⊥BD,CE⊥BD.?∴BD⊥面AEC.?
∴BD⊥AC,故①正确.?
设正方形边长为a,则AD=DC=a,AE=
a=EC.
∴AC=a.?
∴△ACD为等边三角形,故②正确.?
∠ABD为AB与面BCD所成的角为45°,故③不正确.?
以E为坐标原点,EC、ED、EA分别为x,y,z轴建立直角坐标系,?
则A(0,0,
a),B(0,-
a,0),D(0,
a,0),C(
a,0,0).
=(0,-
a,-
a),
=(
a,-
a,0).
cos<
,
>=
=
,
∴<
,
>=60°,故④正确.
故答案为:①②④.
 解:取BD的中点E,则AE⊥BD,CE⊥BD.?∴BD⊥面AEC.?
解:取BD的中点E,则AE⊥BD,CE⊥BD.?∴BD⊥面AEC.?∴BD⊥AC,故①正确.?
设正方形边长为a,则AD=DC=a,AE=
| ||
| 2 |
∴AC=a.?
∴△ACD为等边三角形,故②正确.?
∠ABD为AB与面BCD所成的角为45°,故③不正确.?
以E为坐标原点,EC、ED、EA分别为x,y,z轴建立直角坐标系,?
则A(0,0,
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| AB |
| ||
| 2 |
| ||
| 2 |
| DC |
| ||
| 2 |
| ||
| 2 |
cos<
| AB |
| DC |
| ||
| a2 |
| 1 |
| 2 |
∴<
| AB |
| DC |
故答案为:①②④.
点评:本题考查的知识点是线面垂直的判定与性质,空间两点距离,线面夹角,异面直线的夹角,其中根据已知条件将正方形ABCD沿对角线BD折成直二面角A-BD-C,结合立体几何求出相关直线与直线、直线与平面的夹角,及线段的长是关键,是中档题.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
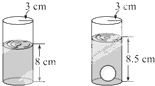 一个圆柱形的玻璃瓶的内半径为3cm,瓶里所装的水深为8cm,将一个钢球完全浸入水中,瓶中水的高度上升到8.5cm,则钢球的半径为( )
一个圆柱形的玻璃瓶的内半径为3cm,瓶里所装的水深为8cm,将一个钢球完全浸入水中,瓶中水的高度上升到8.5cm,则钢球的半径为( )| A、1 cm |
| B、1.2 cm |
| C、1.5 cm |
| D、2 cm |
近期由于某些原因,国内进口豪华轿车纷纷降价,某豪车原价为200万元,连续两次降价a%后,售价为148万元,则下面所列方程正确的是( )
| A、200(1+a%)2=148 |
| B、200(1-a%)2=148 |
| C、200(1-2a%)=148 |
| D、200(1-a%)=148 |
设函数f(x)是偶函数,且当x>0时,f(x)=
,则在区间[-4,-2]内,函数f(x)( )
| 2 |
| x+1 |
A、单调递增,最大值
| ||
B、单调递减,最大值
| ||
C、单调递增,最小值
| ||
D、单调递增,最大值
|
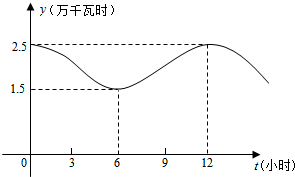 某大型企业一天中不同时刻的用电量y(单位:万千瓦时)关于时间t(0≤t≤24,单位:小时)的函数y=f(t)近似地满足f(t)=Asin(ωt+φ)+B(A>0,ω>0,0<φ<π),如图是该企业一天中在0点至12点时间段用电量y与时间t的大致图象.
某大型企业一天中不同时刻的用电量y(单位:万千瓦时)关于时间t(0≤t≤24,单位:小时)的函数y=f(t)近似地满足f(t)=Asin(ωt+φ)+B(A>0,ω>0,0<φ<π),如图是该企业一天中在0点至12点时间段用电量y与时间t的大致图象.