题目内容
已知椭圆的中心在原点,离心率为
,若F为左焦点,A为右顶点,B为短轴的一个端点,求tan∠ABF的值.
| ||
| 2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:首先,根据椭圆中的参数的意义,可以设OF=c,OA=a,OB=b,然后,根据tan∠ABF=-tan(∠BAF+∠BFA),求解tan∠ABF的值.
解答:
解:设OF=c,OA=a,OB=b,
∴tan∠BAF=
=
,
tan∠BFA=
=
,
∵tan∠ABF=-tan(∠BAF+∠BFA)
=-
=-
∵e2=
=
,
∴a2=2c2,
∵b2=a2-c2=c2
∴ca=
b2,
∴tan∠ABF=-
=-3-2
.
∴tan∠ABF的值-3-2
.
∴tan∠BAF=
| OB |
| OA |
| b |
| a |
tan∠BFA=
| OB |
| OC |
| b |
| c |
∵tan∠ABF=-tan(∠BAF+∠BFA)
=-
| ||||
1-
|
=-
| bc+ab |
| ac-b2 |
∵e2=
| c2 |
| a2 |
| 1 |
| 2 |
∴a2=2c2,
∵b2=a2-c2=c2
∴ca=
| 2 |
∴tan∠ABF=-
b2+
| ||
|
| 2 |
∴tan∠ABF的值-3-2
| 2 |
点评:本题重点考查了椭圆的简单几何性质、两角和与差的正切公式等,属于中档题.理解清晰椭圆中的参数的几何意义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若
=
,
=
,则∠AOB的平分线上的向量
为( )
| OA |
| a |
| OB |
| b |
| OC |
A、
| ||||||||||||||
B、
| ||||||||||||||
C、λ(
| ||||||||||||||
D、
|
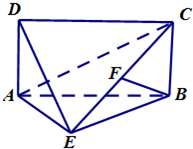 如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.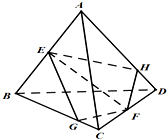 如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面
如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面



