题目内容
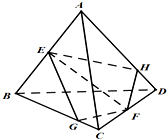 如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面
如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,下列判断中:
①对于任意的平面α,都有S△EFG=S△EFH;
②存在一个平面α0,使得点G在线段BC上,点H在线段AD的延长线上;
③对于任意的平面α,都有直线GF,EH,BD相交于同一点或相互平行;
④对于任意的平面α,当G,H在线段BC,AD上时,几何体AC-EGFH的体积是一个定值.
其中正确的序号是( )
| A、①③④ | B、③④ |
| C、②③ | D、①②③ |
考点:命题的真假判断与应用
专题:阅读型,空间位置关系与距离,简易逻辑
分析:①分别取AC、BD的中点M、N,则BC∥平面MENF,AD∥平面MENF,且AD与BC到平面MENF的距离相等,即可判断;
②不存在一个平面α0,使得点G在线段BC上,点H在线段AD的延长线上,即可判断;
③取AD的中点H,BC的中点G,则EGFH在一个平面内,此时直线GF∥EH∥BD,若GF,EH相交于M,则由公理2和公理1,可得BD也过点M.即可判断;
④对于任意的平面α,当G,H在线段BC,AD上时,可以证明几何体AC-EGFH的体积是四面体ABCD体积的一半.
②不存在一个平面α0,使得点G在线段BC上,点H在线段AD的延长线上,即可判断;
③取AD的中点H,BC的中点G,则EGFH在一个平面内,此时直线GF∥EH∥BD,若GF,EH相交于M,则由公理2和公理1,可得BD也过点M.即可判断;
④对于任意的平面α,当G,H在线段BC,AD上时,可以证明几何体AC-EGFH的体积是四面体ABCD体积的一半.
解答:
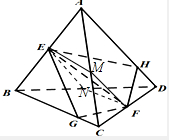 解:①分别取AC、BD的中点M、N,则BC∥平面MENF,AD∥平面MENF,
解:①分别取AC、BD的中点M、N,则BC∥平面MENF,AD∥平面MENF,
且AD与BC到平面MENF的距离相等,因此对于任意的平面α,
都有S△EFG=S△EFH.故①对;
②不存在一个平面α0,使得点G在线段BC上,点H在线段AD的延长线上,
故②错;
③取AD的中点H,BC的中点G,则EGFH在一个平面内,此时直线GF∥EH∥BD;若GF,EH相交于M,则由公理2和公理1,可得BD也过点M,因此③正确;
④对于任意的平面α,当G,H在线段BC,AD上时,由①可以证明几何体AC-EGFH的体积是四面体ABCD体积的一半,因此是一个定值.
综上可知:只有①③④正确.
故选A.
 解:①分别取AC、BD的中点M、N,则BC∥平面MENF,AD∥平面MENF,
解:①分别取AC、BD的中点M、N,则BC∥平面MENF,AD∥平面MENF,且AD与BC到平面MENF的距离相等,因此对于任意的平面α,
都有S△EFG=S△EFH.故①对;
②不存在一个平面α0,使得点G在线段BC上,点H在线段AD的延长线上,
故②错;
③取AD的中点H,BC的中点G,则EGFH在一个平面内,此时直线GF∥EH∥BD;若GF,EH相交于M,则由公理2和公理1,可得BD也过点M,因此③正确;
④对于任意的平面α,当G,H在线段BC,AD上时,由①可以证明几何体AC-EGFH的体积是四面体ABCD体积的一半,因此是一个定值.
综上可知:只有①③④正确.
故选A.
点评:本题考查了线面平行的判定与性质定理、三角形的中位线定理,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
已知函数f(x)是R上的增函数,A(0,-2),B(4,2)是其图象上的两点,那么|f(
)|<2的解集是( )
| 1 |
| 2x+1 |
| A、(1,4) |
| B、(1,+∞) |
| C、(-∞,1)∪[4,+∞] |
| D、(-3,+∞) |
函数y=2sin(2x-
)(x∈[0,π])在下列哪个区间上单调递增( )
| π |
| 6 |
A、[
| ||||
B、[
| ||||
C、[0,
| ||||
| D、[0,π] |
已知函数f(x)=x3+(a+1)x2+(a+1)x+a,在其定义域内既有极大值又有极小值,则实数a的取值范围是( )
| A、-1<a<2 |
| B、a>2或a<-1 |
| C、a<-1 |
| D、a>2 |