题目内容
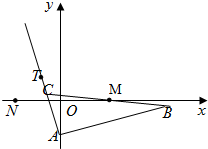 已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足BM=MC,点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.
已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足BM=MC,点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.(1)求AC边所在直线的方程;
(2)求△ABC外接圆的方程.
考点:直线的一般式方程,正弦定理
专题:直线与圆
分析:(1)kAC=-
=-3,由此能求出直线AC的方程..
(2)△ABC外接圆的圆心M(2,0),由
,得A(0,-2),半径r=|AM|,由此能求出△ABC外接圆的方程.
| 1 |
| kAB |
(2)△ABC外接圆的圆心M(2,0),由
|
解答:
解:(1)∵△ABC的边AB边所在直线的方程为x-3y-6=0,
点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.
∴kAC=-
=-3,
∴直线AC:y-1=-3(x+1),整理,得3x+y+2=0.
(2)∵M(2,0)满足BM=MC,点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.
∴△ABC外接圆的圆心M(2,0),
由
,得A(0,-2),
半径r=|AM|=
=2
,
∴△ABC外接圆的方程为(x-2)2+y2=8.
点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.
∴kAC=-
| 1 |
| kAB |
∴直线AC:y-1=-3(x+1),整理,得3x+y+2=0.
(2)∵M(2,0)满足BM=MC,点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.
∴△ABC外接圆的圆心M(2,0),
由
|
半径r=|AM|=
| 4+4 |
| 2 |
∴△ABC外接圆的方程为(x-2)2+y2=8.
点评:本题考查直线方程的求法,考查圆的方程的求法,是基础题,解题时要认真审题,注意两点间距离公式的合理运用.

练习册系列答案
相关题目
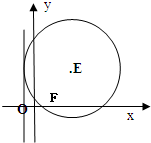 动圆E过点F(1,0),且与直线x=-1相切,圆心E的轨迹是曲线C.
动圆E过点F(1,0),且与直线x=-1相切,圆心E的轨迹是曲线C.