题目内容
(1)若x>1,求x+
的最小值.
(2)设0<x<1,a>0,b>0,a,b为常数,求
+
的最小值.
| 1 |
| x-1 |
(2)设0<x<1,a>0,b>0,a,b为常数,求
| a2 |
| x |
| b2 |
| 1-x |
考点:基本不等式
专题:计算题,不等式的解法及应用
分析:(1)x+
=x-1+
+1,运用基本不等式可求函数的最小值;
(2)
+
=(
+
)(x+1-x)=a2+
+
+b2,运用基本不等式可求函数的最值;
| 1 |
| x-1 |
| 1 |
| x-1 |
(2)
| a2 |
| x |
| b2 |
| 1-x |
| a2 |
| x |
| b2 |
| 1-x |
| (1-x)a2 |
| x |
| xb2 |
| 1-x |
解答:
解:(1)∵x>1,∴x-1>0,
∴x+
=x-1+
+1≥3(当且仅当x-1=
即x=2时取“=”),
∴x+
的最小值为3;
(2)∵0<x<1,a>0,b>0,
∴
+
=(
+
)(x+1-x)=a2+
+
+b2≥a2+2
+b2=(a+b)2,
(当且仅当
=
即x=
时取等号).
∴
+
的最小值是(a+b)2.
∴x+
| 1 |
| x-1 |
| 1 |
| x-1 |
| 1 |
| x-1 |
∴x+
| 1 |
| x-1 |
(2)∵0<x<1,a>0,b>0,
∴
| a2 |
| x |
| b2 |
| 1-x |
| a2 |
| x |
| b2 |
| 1-x |
| (1-x)a2 |
| x |
| xb2 |
| 1-x |
| a2b2 |
(当且仅当
| (1-x)a2 |
| x |
| xb2 |
| 1-x |
| a |
| a+b |
∴
| a2 |
| x |
| b2 |
| 1-x |
点评:该题考查利用基本不等式求函数的最值,属基础题,对式子进行灵活变形,合理创建使用基本不等式的条件是解题关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
如图,该程序运行后输出的结果S为( )


| A、1 | B、10 | C、19 | D、28 |
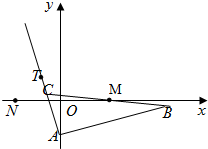 已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足BM=MC,点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.
已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足BM=MC,点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.