题目内容
已知抛物线C;y2=2px(p>0)过点A(1,-2);
(1)求抛物线C的方程,并求其准线方程;
(2)是否存在平行于OA(O为坐标原点)的直线l,使直线l与抛物线C有公共点,直线OA与l的距离等于
?若存在,求出直线l的方程,说明理由.
(1)求抛物线C的方程,并求其准线方程;
(2)是否存在平行于OA(O为坐标原点)的直线l,使直线l与抛物线C有公共点,直线OA与l的距离等于
| ||
| 5 |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)将(1,-2)代入抛物线方程求得p,则抛物线方程可得,进而根据抛物线的性质求得其准线方程.
(2)先假设存在符合题意的直线,设出其方程,与抛物线方程联立,根据直线与抛物线方程有公共点,求得t的范围,利用直线AO与L的距离,求得t,则直线l的方程可得.
(2)先假设存在符合题意的直线,设出其方程,与抛物线方程联立,根据直线与抛物线方程有公共点,求得t的范围,利用直线AO与L的距离,求得t,则直线l的方程可得.
解答:
解:(1)将(1,-2)代入y2=2px,
得(-2)2=2p•1,所以p=2.
故所求的抛物线C的方程为y2=4x,其准线方程为x=-1.
(2)假设存在符合题意的直线l,
其方程为y=-2x+t,代入抛物线方程得y2+2y-2t=0.
因为直线l与抛物线C有公共点,
所以△=4+8t≥0,解得t≥-
.
另一方面,由直线OA到l的距离d=
可得
=
,解得t=±1.
因为-1∉[-
,+∞),1∈[-
,+∞),
所以符合题意的直线l存在,其方程为2x+y-1=0.
得(-2)2=2p•1,所以p=2.
故所求的抛物线C的方程为y2=4x,其准线方程为x=-1.
(2)假设存在符合题意的直线l,
其方程为y=-2x+t,代入抛物线方程得y2+2y-2t=0.
因为直线l与抛物线C有公共点,
所以△=4+8t≥0,解得t≥-
| 1 |
| 2 |
另一方面,由直线OA到l的距离d=
| ||
| 5 |
可得
| |t| | ||
|
| 1 | ||
|
因为-1∉[-
| 1 |
| 2 |
| 1 |
| 2 |
所以符合题意的直线l存在,其方程为2x+y-1=0.
点评:本题小题主要考查了直线,抛物线等基础知识,考查推理论证能力,运算求解能力,考查函数与方程思想,数形结合的思想,化归与转化思想,分类讨论与整合思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
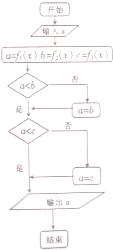 已知函数f1(x)=x,f2(x)=
已知函数f1(x)=x,f2(x)=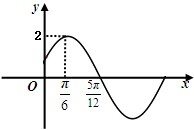 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<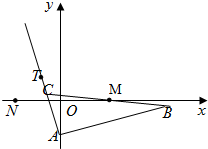 已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足BM=MC,点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.
已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足BM=MC,点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.