题目内容
已知函数f(x)=Asin(ωx+φ),其中A>0,ω>0,0<φ<
,已知的最小正周期是π,最小值为-3,且f(0)=
.
(1)求f(x)的解析式;
(2)求不等式f(x)≥
的解集;
(3)如何由f(x)的图象得到函数y=sin4x的图象?
| π |
| 2 |
| 3 |
| 2 |
(1)求f(x)的解析式;
(2)求不等式f(x)≥
3
| ||
| 2 |
(3)如何由f(x)的图象得到函数y=sin4x的图象?
考点:函数y=Asin(ωx+φ)的图象变换,由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(1)由函数的图象的顶点坐标求出A,由周期求出ω,由特殊点的坐标求出φ的值,可得函数的解析式.
(2)由不等式可得sin(2x+
)≥
,令 2kπ+
≤2x+
≤2kπ+
,k∈z,求出x的范围,即为所求.
(3)根据函数y=Asin(ωx+φ)的图象变换规律,得出结论.
(2)由不等式可得sin(2x+
| π |
| 6 |
| ||
| 2 |
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
(3)根据函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答:
解:(1)对于函数f(x)=Asin(ωx+φ),由函数的最小正周期是
=π,可得ω=2.
根据函数的最小值为-3,可得A=3.由f(0)=3sinφ=
,可得 sinφ=
,
再结合0<φ<
,可得φ=
,故函数的解析式为f(x)=3sin(2x+
).
(2)由不等式f(x)≥
可得,sin(2x+
)≥
,令 2kπ+
≤2x+
≤2kπ+
,k∈z,
求得 kπ+
≤x≤kπ+
,故不等式的解集为 {x|kπ+
≤x≤kπ+
,k∈Z}.
(3)把f(x)的图象向右平移
个单位,可得y=3sin[2(x-
)+
]=3sin2x的图象,
再把素的图象的横坐标变为原来的
倍,可得函数y=sin4x的图象.
| 2π |
| ω |
根据函数的最小值为-3,可得A=3.由f(0)=3sinφ=
| 3 |
| 2 |
| 1 |
| 2 |
再结合0<φ<
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
(2)由不等式f(x)≥
3
| ||
| 2 |
| π |
| 6 |
| ||
| 2 |
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
求得 kπ+
| π |
| 12 |
| π |
| 4 |
| π |
| 12 |
| π |
| 4 |
(3)把f(x)的图象向右平移
| π |
| 12 |
| π |
| 12 |
| π |
| 6 |
再把素的图象的横坐标变为原来的
| 1 |
| 2 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,函数y=Asin(ωx+φ)的图象变换规律,三角不等式的解法,属于及撤退.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设数列{an}是单调递增的等差数列,前三项的和为12,前三项的积为48,则a1=( )
| A、1 | B、2 | C、±2 | D、4 |
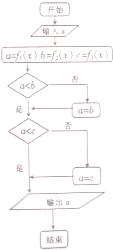
如图,该程序运行后输出的结果S为( )


| A、1 | B、10 | C、19 | D、28 |
 已知函数f1(x)=x,f2(x)=
已知函数f1(x)=x,f2(x)=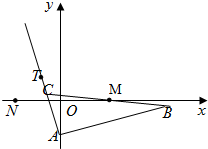 已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足BM=MC,点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.
已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足BM=MC,点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.