题目内容
设Sn是等差数列{an}的前n项和,首项为a1,公差d≠0,
(1)用a1,d表示
S3,
S4,
S5,
(2)已知
S3,
S4的等比中项为
S5,
S3,
S4的等差中项为1.求a1,d;
(3)写出{an}的通项公式.
(注:等差数列的前n项和公式为Sn=na1+
d)
(1)用a1,d表示
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
(2)已知
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 4 |
(3)写出{an}的通项公式.
(注:等差数列的前n项和公式为Sn=na1+
| n(n-1) |
| 2 |
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:(1)直接运用等差数列的前n项和公式即可表示;
(2)利用等比中项公式、等差中项公式可得关于a1,d的方程组,解出即可;
(3)直接由等差数列的通项公式可求;
(2)利用等比中项公式、等差中项公式可得关于a1,d的方程组,解出即可;
(3)直接由等差数列的通项公式可求;
解答:
解:(1)
S3=
(3a1+
d)=a1+d,
S4=
(4a1+
d)=a1+
d,
S5=
(5a1+
d)=a1+2d.
(2)∵
S3,
S4的等比中项为
S5,
∴(
S5)2=
S3•
S4,即(a1+2d)2=(a1+d)(a1+
d),化简得3a1+5d=0①,
∵
S3,
S4的等差中项为1,
∴
S3+
S4=2,即(a1+d)+(a1+
d)=2.化简得2a1+
d=2②,
联立①②解得a1=4,d=-
;
(3)由等差数列的通项公式可得an=a1+(n-1)d=4+(n-1)(-
)=-
n+
.
| 1 |
| 3 |
| 1 |
| 3 |
| 3×2 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 4×3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 5 |
| 1 |
| 5 |
| 5×4 |
| 2 |
(2)∵
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
∴(
| 1 |
| 5 |
| 1 |
| 3 |
| 1 |
| 4 |
| 3 |
| 2 |
∵
| 1 |
| 3 |
| 1 |
| 4 |
∴
| 1 |
| 3 |
| 1 |
| 4 |
| 3 |
| 2 |
| 5 |
| 2 |
联立①②解得a1=4,d=-
| 12 |
| 5 |
(3)由等差数列的通项公式可得an=a1+(n-1)d=4+(n-1)(-
| 12 |
| 5 |
| 12 |
| 5 |
| 32 |
| 5 |
点评:该题考查等差数列的通项公式、前n项和公式,属基础题,熟记相关公式是解题关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
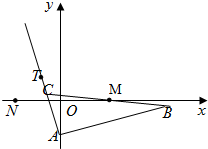 已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足BM=MC,点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.
已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足BM=MC,点T(-1,1)在AC边所在直线上且满足lAB⊥lAT.