题目内容
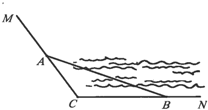如图，CM，CN为某公园景观湖胖的两条木栈道，∠MCN=120°，现拟在两条木栈道的A，B处设置观景台，记BC=a，AC=b，AB=c（单位：百米）（1）若a，b，c成等差数列，且公差为4，求b的值；
（2）已知AB=12，记∠ABC=θ，试用θ表示观景路线A-C-B的长，并求观景路线A-C-B长的最大值．
考点：解三角形的实际应用
专题：应用题,解三角形
分析：（1）利用a，b，c成等差数列，且公差为4，结合余弦定理，即可求b的值；
（2）利用正弦定理，求出AC，BC，再化简，即可求观景路线A-C-B长的最大值．
（2）利用正弦定理，求出AC，BC，再化简，即可求观景路线A-C-B长的最大值．
解答：
解：（1）∵a，b，c成等差数列，且公差为4，∴a=b-4，c=b+4，
∵∠MCN=120°，
∴（b+4）2=（b-4）2+b-2b（b-4）cos120°，
∴b=20；
（2）由题意，
=
=
，
∴AC=8
sinθ，BC=8
sin（60°-θ），
∴观景路线A-C-B的长y=12+8
sinθ+8
sin（60°-θ）=12+8
sin（60°+θ）
∴θ=30°时，观景路线A-C-B长的最大值为12+8
．
∵∠MCN=120°，
∴（b+4）2=（b-4）2+b-2b（b-4）cos120°，
∴b=20；
（2）由题意，
| AC |
| sinθ |
| BC |
| sin(60°-θ) |
| 12 |
| sin120° |
∴AC=8
| 3 |
| 3 |
∴观景路线A-C-B的长y=12+8
| 3 |
| 3 |
| 3 |
∴θ=30°时，观景路线A-C-B长的最大值为12+8
| 3 |
点评：本题考查余弦定理、正弦定理的运用，考查三角函数知识，正确运用正弦、余弦定理是关键．
练习册系列答案
金钥匙试卷系列答案
相关题目
R表示实数集，集合M={x|0≤x≤2}，N={x|x2-3x-4＞0}，则下列结论正确的是（ ）
| A、M⊆N |
| B、（∁RM）⊆N |
| C、M⊆（∁RN） |
| D、（∁RM）⊆（∁RN） |
若x2＞x1＞1则（ ）
| A、e x1-x2＜lgx1-lgx2 | ||
B、e
| ||
| C、x1 x2＞x2 x1 | ||
| D、x1 x2＜x2 x1 |
下列结论中正确的是（ ）
| A、若两个变量的线性相关性越强，则相关系数的绝对值越接近于0 |
| B、在某项测量中，测量结果ξ服从正态分布N（1，σ2）（σ＞0），若ξ位于区域（0，1）的概率为0.4，则ξ位于区域（1，+∞）内的概率为0.6 |
| C、从匀速传递的产品生产流水线上，质检员每4'分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样 |
| D、利用随机变量Χ2来判断“两个独立事件X，Y的关系”时，算出的Χ2值越大，判断“X与Y有关”的把握就越大 |