题目内容
设函数f(x)=x2+bx+c,若函数y=|f(x)|在区间[-1,1]上的最大值是M,求证:M≥
.
| 1 |
| 2 |
考点:二次函数在闭区间上的最值,二次函数的性质
专题:函数的性质及应用
分析:把函数|f(x)|=g(x)配方,然后分|b|>2时,|b|≤2时,由函数y=|f(x)|的单调性求出其最大值,又g(b)=|b2+c|,再分当-2≤b≤0时和0<b≤2时,求出最大值M,经比较可知对任意的b、c都有M≥
.
| 1 |
| 2 |
解答:
解:设|f(x)|=g(x),
当|b|≤2时,函数y=g(x)的对称轴x=-
位于区间[-1,1]之内,
此时M=max{g(-1),g(1),g(b)},
又g(b)=|2b2+c|,
①当-2≤b≤0时,有f(1)≤f(-1)≤f(b),
则M=max{g(b),g(1)}≥
[g(b)+g(1)]≥
|f(b)-f(1)|=
(b-
)2≥
;
②当0<b≤2时,有f(-1)≤f(1)≤f(b).
则M=max{g(b),g(-1)}≥
(g(b)+g(-1))≥
|f(b)-f(-1)|=
(b-
)2≥
;
综上可知,对任意的b、c都有M≥
.
当|b|≤2时,函数y=g(x)的对称轴x=-
| b |
| 2 |
此时M=max{g(-1),g(1),g(b)},
又g(b)=|2b2+c|,
①当-2≤b≤0时,有f(1)≤f(-1)≤f(b),
则M=max{g(b),g(1)}≥
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②当0<b≤2时,有f(-1)≤f(1)≤f(b).
则M=max{g(b),g(-1)}≥
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综上可知,对任意的b、c都有M≥
| 1 |
| 2 |
点评:本题考查二次函数及其应用,以及利用函数单调性求函数的最值,考查了分类讨论.

练习册系列答案
相关题目
已知f(x)=-x3-x+c,若实数a,b,当a+b≤0,则下列正确的是( )
| A、f(a)+f(b)≤-[f(a)+f(b)] |
| B、f(a)+f(b)≤f(-a)+f(-b) |
| C、f(a)+f(b)≥-[f(a)+f(b)] |
| D、f(a)+f(b)≥f(-a)+f(-b) |
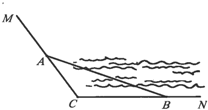 如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)
如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米) 函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象的一部分如图所示,
函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象的一部分如图所示,