题目内容
已知:a1=1,an+1-an=n,求{an}通项公式.
考点:数列递推式
专题:计算题,等差数列与等比数列
分析:根据已知,{an+1-an}是一个等差数列,即可得出结论.
解答:
解:n≥2,an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=(n-1)+…+2+1+1
=
+1,
n=1时,也成立,
所以数列{an}的通项公式为an=
+1.
=(n-1)+…+2+1+1
=
| n(n-1) |
| 2 |
n=1时,也成立,
所以数列{an}的通项公式为an=
| n(n-1) |
| 2 |
点评:本题主要考查由递推公式推导数列的通项公式,通过变形我们要发现数列的规律,转化到等差或等比数列上来,就会很容易解决问题.

练习册系列答案
相关题目
已知f(x)=-x3-x+c,若实数a,b,当a+b≤0,则下列正确的是( )
| A、f(a)+f(b)≤-[f(a)+f(b)] |
| B、f(a)+f(b)≤f(-a)+f(-b) |
| C、f(a)+f(b)≥-[f(a)+f(b)] |
| D、f(a)+f(b)≥f(-a)+f(-b) |
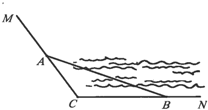 如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)
如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)