题目内容
已知[x]表示不超过x的最大整数,例如[-1.5]=-2,[1.2]=1.设函数f(x)=[x[x]],当x∈[0,n),(n∈N*)时,函数f(x)的值域为集合A,则A中的元素个数为 .
考点:元素与集合关系的判断
专题:集合
分析:根据[x]的定义,分别进行讨论即可得到结论.
解答:
解:根据题意,可得:
[0,n)=[0,1)∪[1,2)∪[2,3)∪…[n-1,n),
当x∈[0,1),[x[x]]=[x•0]=0,只有1个,
当x∈[1,2),[x[x]]=[x]=1,只有1个,
当x∈[2,3),[x[x]]=[2x]∈{4,5},有2个,
当x∈[3,4),[x[x]]=[3x]∈{9,10,11},有3个,
…
当x∈[n-1,n)时,
[x[x]]=[(n-1)x]∈{(n-1)2,(n-1)2+1,(n-1)2+2,…,n(n-1)-1},
共有n(n-1)-(n-1)2=n-1个,
∴所有A中的元素个数为1+1+2+3+4+…+(n-1)=
(n2-n+2),
故答案为:
(n2-n+2).
[0,n)=[0,1)∪[1,2)∪[2,3)∪…[n-1,n),
当x∈[0,1),[x[x]]=[x•0]=0,只有1个,
当x∈[1,2),[x[x]]=[x]=1,只有1个,
当x∈[2,3),[x[x]]=[2x]∈{4,5},有2个,
当x∈[3,4),[x[x]]=[3x]∈{9,10,11},有3个,
…
当x∈[n-1,n)时,
[x[x]]=[(n-1)x]∈{(n-1)2,(n-1)2+1,(n-1)2+2,…,n(n-1)-1},
共有n(n-1)-(n-1)2=n-1个,
∴所有A中的元素个数为1+1+2+3+4+…+(n-1)=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查与集合有关的新定义题,根据条件分别求出对应范围的个数是解决本题的关键,综合性较强,属中档题.

练习册系列答案
相关题目
已知f(x)=-x3-x+c,若实数a,b,当a+b≤0,则下列正确的是( )
| A、f(a)+f(b)≤-[f(a)+f(b)] |
| B、f(a)+f(b)≤f(-a)+f(-b) |
| C、f(a)+f(b)≥-[f(a)+f(b)] |
| D、f(a)+f(b)≥f(-a)+f(-b) |
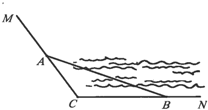 如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米)
如图,CM,CN为某公园景观湖胖的两条木栈道,∠MCN=120°,现拟在两条木栈道的A,B处设置观景台,记BC=a,AC=b,AB=c(单位:百米) 函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象的一部分如图所示,
函数y=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象的一部分如图所示, 设函数f(x)=|x+2|+|2x-4|,g(x)=a+x.
设函数f(x)=|x+2|+|2x-4|,g(x)=a+x.