题目内容
计算：log
2
-log23•log32= ．
| 2 |
| 2 |
考点：对数的运算性质
专题：函数的性质及应用
分析：利用对数的运算性质、对数的换底公式即可得出．
解答：
解：原式=log
(
)3-log23•
=3-1=2，
故答案为：2．
| 2 |
| 2 |
| 1 |
| log32 |
故答案为：2．
点评：本题考查了对数的运算性质、对数的换底公式，属于基础题．
练习册系列答案
相关题目
抛物线y2=8x的焦点到双曲线x2-
=1的一条渐近线的距离为（ ）
| y2 |
| 3 |
| A、1 | ||
| B、2 | ||
C、
| ||
D、2
|
设复数z满足（1+i）z=1-i，其中i为虚数单位，则z=（ ）
| A、-i | B、i | C、-1 | D、1 |
若P={y|y=|x|}，Q={x|-
≤x≤
}，则P∩Q=（ ）
| 2 |
| 2 |
A、（0，
| ||||
| B、{（1，1），（-1，-1）} | ||||
C、[0，
| ||||
D、（-
|
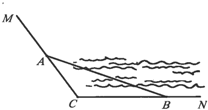如图，CM，CN为某公园景观湖胖的两条木栈道，∠MCN=120°，现拟在两条木栈道的A，B处设置观景台，记BC=a，AC=b，AB=c（单位：百米）
函数y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象的一部分如图所示，