题目内容
R表示实数集，集合M={x|0≤x≤2}，N={x|x2-3x-4＞0}，则下列结论正确的是（ ）
| A、M⊆N |
| B、（∁RM）⊆N |
| C、M⊆（∁RN） |
| D、（∁RM）⊆（∁RN） |
考点：交、并、补集的混合运算
专题：集合
分析：化简集合N为{x|x＜-1，或x＞4}，分别写出∁RM，∁RN即可．
解答：
解：∵x2-3x-4=（x-4）（x+1）＞0
∴N={x|x＜-1或x＞4}，
则∁RM={x|x＜0或x＞2}，
∁RN={x|-1≤x≤4}，
又集合M={x|0≤x≤2}，
所以M⊆∁RN，
故选：C．
∴N={x|x＜-1或x＞4}，
则∁RM={x|x＜0或x＞2}，
∁RN={x|-1≤x≤4}，
又集合M={x|0≤x≤2}，
所以M⊆∁RN，
故选：C．
点评：本题考查集合的运算，解题时要认真审题，属基础题．
练习册系列答案
相关题目
抛物线y2=8x的焦点到双曲线x2-
=1的一条渐近线的距离为（ ）
| y2 |
| 3 |
| A、1 | ||
| B、2 | ||
C、
| ||
D、2
|
定义在R上的函数的图象关于直线x=
对称，且对任意的实数x都有f（x）=-f（x+
），f（-1）=1，f（0）=-2，则f（2013）+f（2014）+f（2015）=（ ）
| 3 |
| 2 |
| 3 |
| 2 |
| A、0 | B、-2 | C、1 | D、2 |
在平面直角坐标系xOy中，双曲线的中心在原点，焦点在y轴上，一条渐近线方程为x-2y=0，则它的离心率为（ ）
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
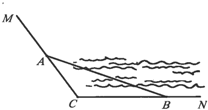如图，CM，CN为某公园景观湖胖的两条木栈道，∠MCN=120°，现拟在两条木栈道的A，B处设置观景台，记BC=a，AC=b，AB=c（单位：百米）