题目内容
2.已知向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(2,-3),且(k$\overrightarrow{a}$-$\overrightarrow{b}$)∥($\overline{a}$+3$\overrightarrow{b}$),则实数k等于-$\frac{1}{3}$.分析 根据平面向量的坐标运算与向量平行的坐标表示,列出方程求出解即可.
解答 解:∵向量$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(2,-3),
∴k$\overrightarrow{a}$-$\overrightarrow{b}$=(2k-2,k+3)
$\overline{a}$+3$\overrightarrow{b}$=(8,-8),
又(k$\overrightarrow{a}$-$\overrightarrow{b}$)∥($\overline{a}$+3$\overrightarrow{b}$),
∴-8(2k-2)-8(k+3)=0,
解得k=$-\frac{1}{3}$.
故答案为:-$\frac{1}{3}$.
点评 本题考查了平面向量的坐标运算与应用问题,也考查了向量共线的应用问题,是基础题目.

练习册系列答案
相关题目
19.已知cos2α=$\frac{1}{3}$,则$\frac{tan2α}{tanα}$的值为( )
| A. | -4 | B. | -$\frac{1}{4}$ | C. | 4 | D. | $\frac{1}{4}$ |
7.A={x|0<x<2},$B=\left\{{x|y=\sqrt{x-1}}\right\}$,则A∩B( )
| A. | (0,1) | B. | (0,1] | C. | (1,2) | D. | [1,2) |
11.函数$y=\frac{{\sqrt{x}}}{x-1}$的定义域为( )
| A. | [0,1)∪(1,+∞) | B. | (0,+∞) | C. | (0,1) | D. | [0,1] |
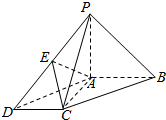 在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.
在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.