题目内容
14.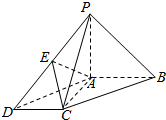 在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.
在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.(1)求证:PB∥平面AEC;
(2)求证:平面EAC⊥平面PAB.
分析 (1)连接BD交AC于F,连接EF,利用三角形的中位线定理证明EF∥PB,再证明PB∥平面AEC;
(2)利用线面垂直的定义得出PA⊥AC,再证明AC⊥平面PAB与平面EAC⊥平面PAB.
解答 证明:(1)如图所示,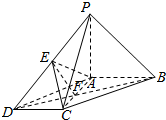
连接BD交AC于F,连接EF,
在△DPB中,EF为中位线,
∴EF∥PB;
又PB?平面EAC,EF?平面EAC,
∴PB∥平面AEC;
(2)∵PA⊥平面ABCD,AC?平面ABCD,
∴PA⊥AC;
又AB⊥AC,PA∩AB=A,
∴AC⊥平面PAB;
又AC?平面EAC,
∴平面EAC⊥平面PAB.
点评 本题考查了空间中的平行与垂直关系的应用问题,也考查了逻辑推理与证明能力,是中档题目.

练习册系列答案
相关题目
6.在本埠投寄平信,每封信不超过20g时付邮资0.80元,超过20g而不超过40g时付邮资1.60元,依此类推,每增加20g需增加邮资0.80元(信重在100g以内),如果某人所寄的一封信的重量为82.5g,那么他应付邮资( )
| A. | 2.4元 | B. | 2.8元 | C. | 3.2元 | D. | 4元 |
7.已知f(x)是偶函数,它在[0,+∞)上是减函数,若f(ex)≥f(-e),则x的取值范围是( )
| A. | R | B. | (-∞,-1]∪[1,+∞) | C. | (-∞,1] | D. | [-1,1] |
9.已知α,β均为锐角,cosα=$\frac{1}{7}$,cos(α+β)=-$\frac{11}{14}$,则角β为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
19.已知偶函数f(x)的定义域为R,且f(x)在[0,+∞)单调递减,则( )
| A. | f(4)<f(-2)<f(1) | B. | f(1)<f(-2)<f(4) | C. | f(-2)<f(1)<f(4) | D. | f(4)<f(1)<f(-2) |
3.在空间中,a、b、c是三条不同的直线,α、β是两个不同的平面,则下列为真命题的是( )
| A. | 若a∥α,a∥b,b∥c,则c∥α | B. | 若a?α,b?β,α⊥β,则a⊥b | ||
| C. | 若a⊥α,a⊥b,b⊥c,则c⊥α | D. | 若α∥β,a?α,则a∥β |