题目内容
设集合A={x|x2-2x-3<0},B={x|
<2x<4},则A∩B等于( )
| 1 |
| 2 |
| A、{x|-1<x<2} |
| B、{x|-1<x<3} |
| C、{x|-3<x<2} |
| D、{x|-3<x<-1} |
考点:指、对数不等式的解法,交集及其运算,一元二次不等式的解法
专题:不等式的解法及应用
分析:根据不等式的性质求出集合A,B,然后根据集合的基本运算可求A∩B.
解答:
解:∵A={x|x2-2x-3<0}={x|-1<x<3},
B={x|
<2x<4}={x|-1<x<2},
∴A∩B={x|-1<x<2},
故选:A.
B={x|
| 1 |
| 2 |
∴A∩B={x|-1<x<2},
故选:A.
点评:本题主要考查集合的基本运算,利用不等式的解法求出集合A,B是解决本题的关键,比较基础.

练习册系列答案
相关题目
在△ABC中,角A、B、C的对边分别为a,b,c,若a=2,b=3,c=
,则△ABC的形状一定是( )
| 5 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、三角形形状不确定 |
在△ABC中,已知∠A=120°,且
=
,则sinC等于( )
| AC |
| AB |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=log2(4x-x2)的单调递减区间是( )
| A、(0,4) |
| B、(0,2] |
| C、[2,4) |
| D、(2,+∞) |
若偶函数f(x)在(-∞,-1]上是增函数,则下列关系式中成立的是( )
A、f(-
| ||
B、f(π)<f(-
| ||
C、f(π)<f(-1)<f(-
| ||
D、f(-1)<f(-
|
已知一个三角形的三边长分别是5,5,6,一只蚂蚁在其内部爬行,若不考虑蚂蚁的大小,则某时刻该蚂蚁距离三角形的三个顶点的距离均超过2的概率是( )
A、2-
| ||
B、1-
| ||
C、2-
| ||
D、1-
|
 (1)
(1)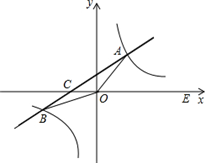 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=
如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=