题目内容
已知函数f(x)=|x-a|
(1)若不等式f(x)≤b的解集为{x|1≤x≤5},求a,b的值
(2)若不等式f(x+a+2)+f(x)≤4的解集非空,求实数a的取值范围.
(1)若不等式f(x)≤b的解集为{x|1≤x≤5},求a,b的值
(2)若不等式f(x+a+2)+f(x)≤4的解集非空,求实数a的取值范围.
考点:其他不等式的解法
专题:不等式的解法及应用
分析:(1)f(x)≤b可化为|x-a|≤b,可得不等式的解集,利用不等式f(x)≤b的解集为{x|1≤x≤5},建立方程组,可求a,b的值;
(2)不等式f(x+a+2)+f(x)≤4等价于不等式|x+2|+|x-a|≤4,求出左边的最小值,即可求实数a的取值范围.
(2)不等式f(x+a+2)+f(x)≤4等价于不等式|x+2|+|x-a|≤4,求出左边的最小值,即可求实数a的取值范围.
解答:
解:(1)f(x)≤b可化为|x-a|≤b,
∴a-b≤x≤a+b,
∵不等式f(x)≤b的解集为{x|1≤x≤5},
∴
,
∴a=3,b=2;
(2)不等式f(x+a+2)+f(x)≤4等价于不等式|x+2|+|x-a|≤4,
由绝对值的意义可得,|x+2|+|x-a|表示数轴上的x对应点与-2,a的距离的和,其最小值为|2+a|,
∴|2+a|≤4,
∴-6≤a≤2.
∴a-b≤x≤a+b,
∵不等式f(x)≤b的解集为{x|1≤x≤5},
∴
|
∴a=3,b=2;
(2)不等式f(x+a+2)+f(x)≤4等价于不等式|x+2|+|x-a|≤4,
由绝对值的意义可得,|x+2|+|x-a|表示数轴上的x对应点与-2,a的距离的和,其最小值为|2+a|,
∴|2+a|≤4,
∴-6≤a≤2.
点评:本题考查不等式的解法,考查学生分析转化问题的能力,正确转化是关键.

练习册系列答案
相关题目
已知函数f(x)=|x2-6|,若a<b<0,且f(a)=f(b),则a2b的最小值是( )
| A、-16 | B、-12 |
| C、-10 | D、-8 |
若直线l:4x+3y+a=0和圆C:x2+y2+2x-4y+1=0有公共点,则实数a的取值范围是( )
| A、[-12,8] |
| B、[-8,12] |
| C、[-22,18] |
| D、[-18,22] |
在△ABC中,角A、B、C的对边分别为a,b,c,若a=2,b=3,c=
,则△ABC的形状一定是( )
| 5 |
| A、锐角三角形 |
| B、直角三角形 |
| C、钝角三角形 |
| D、三角形形状不确定 |
 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为
如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为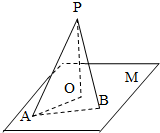 如图,直线PO⊥平面M,垂足为O,直线PA是平面M的一条斜线,斜足为A,其中∠APO=α,过点P的动直线PB交平面M于点B,∠APB=β,则下列说法正确的是
如图,直线PO⊥平面M,垂足为O,直线PA是平面M的一条斜线,斜足为A,其中∠APO=α,过点P的动直线PB交平面M于点B,∠APB=β,则下列说法正确的是 (1)
(1)