题目内容
已知关于x的方程|x2-2x|+m=0(m≤0)的解集为M,则集合M中所有的元素的和的最大值为 .
考点:其他不等式的解法
专题:不等式的解法及应用
分析:数形结合可得,函数y=|x2-2x|的图象(红线)和直线 y=-m(蓝线)至多有4个交点,且这4个交点关于直线x=1对称,此时,方程的解集M中所有的元素的和的最大值,再利用二次函数的性质求得集合M中所有的元素的和的最大值.
解答:
 解:由题意可得方程即|x2-2x|=-m,故函数y=|x2-2x|的图象(红线)和直线 y=-m(蓝线)有交点.
解:由题意可得方程即|x2-2x|=-m,故函数y=|x2-2x|的图象(红线)和直线 y=-m(蓝线)有交点.
由于m≤0,∴-m≥0,如图所示:
函数y=|x2-2x|的图象(红线)和直线 y=-m(蓝线)至少有2个交点,且这两个交点关于直线x=1对称,
此时,方程的解集M中所有的元素的和的最小值为2.
函数y=|x2-2x|的图象(红线)和直线 y=-m(蓝线)至多有4个交点,且这4个交点关于直线x=1对称,
此时,方程的解集M中所有的元素的和的最大值为2+2=4,
故答案为:4.
 解:由题意可得方程即|x2-2x|=-m,故函数y=|x2-2x|的图象(红线)和直线 y=-m(蓝线)有交点.
解:由题意可得方程即|x2-2x|=-m,故函数y=|x2-2x|的图象(红线)和直线 y=-m(蓝线)有交点.由于m≤0,∴-m≥0,如图所示:
函数y=|x2-2x|的图象(红线)和直线 y=-m(蓝线)至少有2个交点,且这两个交点关于直线x=1对称,
此时,方程的解集M中所有的元素的和的最小值为2.
函数y=|x2-2x|的图象(红线)和直线 y=-m(蓝线)至多有4个交点,且这4个交点关于直线x=1对称,
此时,方程的解集M中所有的元素的和的最大值为2+2=4,
故答案为:4.
点评:本题主要考查方程解的个数判断,二次函数的性质,体现了转化以及数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=3x2-(k-2)x-8在[5,10]上具有单调性,则实数k的取值范围是( )
| A、[32,62] |
| B、(-∞,32]∪[62,+∞) |
| C、(32,62) |
| D、(-∞,32)∪(62,+∞) |
已知x、y满足约束条件
,则z=3x+5y的最小值为( )
|
| A、17 | B、-11 |
| C、11 | D、-17 |
若点(a,-1)在函数y=log
x的图象上,则tan
的值为( )
| 1 |
| 2 |
| aπ |
| 6 |
| A、0 | ||||
B、
| ||||
| C、1 | ||||
D、
|
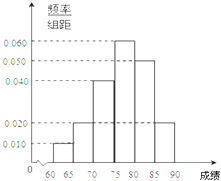 在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,统计了他们的成绩,得到如图所示的频率分布直方图.
在某次综合素质测试中,共设有40个考室,每个考室30名考生.在考试结束后,为调查其测试前的培训辅导情况与测试成绩的相关性,抽取每个考室中座位号为05的考生,统计了他们的成绩,得到如图所示的频率分布直方图. 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为
如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为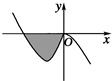 (1)
(1)