题目内容
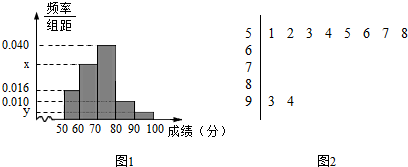
16.为选拔选手参加“中国谜语大全”,某中学举行一次“谜语大赛”活动,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分去正整数,满分为100分)作为样本进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100)的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出得分在[50,60),[90,100)的数据).(Ⅰ)求样本容量n和频率分布直方图中x,y的值;
(Ⅱ)分数在[80,90)的学生中,男生有2人,现从该组抽取三人“座谈”,写出基本事件空间并求至少有两名女生的概率.
分析 (Ⅰ)由频率分布直方图得学生的分数在[50,60)内的频率,由茎叶图得学生的分数在[50,60)内的频数,由此能求出样本容量,由学生的分数在[90,100)内的频数为2,能求出y,从而能求出x.
(Ⅱ)先求出分数在[80,90)的学生的频率,得到分数在[80,90)的学生共有5人,由题意得男生2人,女生3人,由此能写出基本事件空间并求出至少有两名女生的概率
解答 解:(Ⅰ)由频率分布直方图得学生的分数在[50,60)内的频率为0.016×10=0.16,
由茎叶图得学生的分数在[50,60)内的频数为8,
∴样本容量n=$\frac{8}{0.16}$=50,
∵学生的分数在[90,100)内的频数为2,
∴y=$\frac{2}{50×10}$=0.02,
x=0.100-0.004-0.010-0.016-0.040=0.030.
(Ⅱ)∵分数在[80,90)的学生的频率为0.010×10=0.1,
∴分数在[80,90)的学生共有5人,由题意得男生2人,女生3人,
男生的编号为b1,b2,女生的编号a1,a2,a3,
∴基本事件空间为{(a1,a2,a3),(a1,a2,b1),(a1,a2,b2),(a1,a3,b1),(a1,a3,b2),(a2,a3,b1),(a2,a3,b2),(b1,b2,a1),(b1,b2,a2),(b1,b2,a3)},共10个,
记A=“至少有两名女生”,则事件A包含的东奔西走事件数共7个,
∴至少两名女生的概率为P(A)=$\frac{7}{10}$.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
6.一个圆锥的底面半径为2cm,高为6cm,在其中有一个高为3cm的内接圆柱,则圆柱的侧面积为( )
| A. | 2πcm2 | B. | 4πcm2 | C. | 6πcm2 | D. | 12πcm2 |
11.在△ABC中,b=5,c=5$\sqrt{3}$,A=30°,则a等于( )
| A. | 5 | B. | 4 | C. | 3 | D. | 10 |
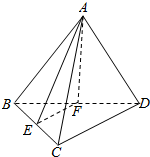 如图,正三棱锥A-BCD的侧棱长为2,底面BCD的边长为2$\sqrt{2}$,E,分别为BC,BD的中点,则三棱锥A-BEF的外接球的半径R=1,内切球半径r=2-$\sqrt{3}$.
如图,正三棱锥A-BCD的侧棱长为2,底面BCD的边长为2$\sqrt{2}$,E,分别为BC,BD的中点,则三棱锥A-BEF的外接球的半径R=1,内切球半径r=2-$\sqrt{3}$.