题目内容
14.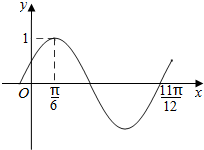 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,若将y=f(x)的图象向右平移m(m>0)个单位后,得到的图象关于原点对称,则m的最小值为( )| A. | $\frac{π}{24}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
分析 利用y=Asin(ωx+φ)的图象特征,求出函数y=Asin(ωx+φ)的解析式,再根据y=Asin(ωx+φ)的图象变换规律及正弦函数的图象和性质,求得m的最小值.
解答 解:由图可知A=2,$\frac{3}{4}$T=$\frac{11π}{12}$-$\frac{π}{6}$,T=π,
∴?=2.
∵由图可得点($\frac{π}{6}$,2)在函数图象上,可得:2sin(2×$\frac{π}{6}$+φ)=2,解得:2×$\frac{π}{6}$+φ=2k$π+\frac{π}{2}$,k∈Z,
∴由|φ|<$\frac{π}{2}$,可得:φ=$\frac{π}{6}$,
∴f(x)=2sin(2x+$\frac{π}{6}$).
若将y=f(x)的图象向右平移m(m>0)个单位后,得到的函数解析式为:y=2sin(2x-2m+$\frac{π}{6}$).
∵得到的图象关于原点对称,
∴-2m+$\frac{π}{6}$=$\frac{kπ}{2}$,k∈Z,解得:m=$\frac{π}{12}$-$\frac{kπ}{4}$,k∈Z,
∵m>0,
∴m的最小值为$\frac{π}{12}$.
故选:B.
点评 本题主要考查y=Asin(ωx+φ)的图象变换规律,由函数y=Asin(ωx+φ)的部分图象求解析式,正弦函数的图象和性质,考查了数形结合思想,属于中档题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
5.若集合$M=\{x|y={log_2}(-{x^2}+x+6)\}$,N={y|y=x2+1,x∈R},则集合M∩N=( )
| A. | (-2,+∞) | B. | (-2,3) | C. | [1,3) | D. | R |
2.下列各数中最小的数为( )
| A. | 101111(2) | B. | 1210(3) | C. | 112(8) | D. | 69(12) |
9.将边长为2的正方形ABCD沿对角线BD折起,使平面ABD⊥平面CBD,则三棱锥C-ABD的外接球表面积为( )
| A. | 16π | B. | 12π | C. | 8π | D. | 4π |
6.一个圆锥的底面半径为2cm,高为6cm,在其中有一个高为3cm的内接圆柱,则圆柱的侧面积为( )
| A. | 2πcm2 | B. | 4πcm2 | C. | 6πcm2 | D. | 12πcm2 |