题目内容
12.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的离心率为2,焦点与椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的焦点相同,那么双曲线的实轴长为4.分析 根据两曲线焦点相同求出c=4,根据离心率为2求出a,则实轴长2a.
解答 解:∵双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的焦点与椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的焦点相同,∴c2=a2+b2=25-9=16,∴c=4,
∵双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的离心率为2,∴a=2,2a=4.即双曲线的实轴长为4.
故答案为4.
点评 本题考查了圆锥曲线的性质,属于基础题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
2.下列各数中最小的数为( )
| A. | 101111(2) | B. | 1210(3) | C. | 112(8) | D. | 69(12) |
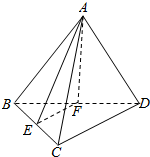 如图,正三棱锥A-BCD的侧棱长为2,底面BCD的边长为2$\sqrt{2}$,E,分别为BC,BD的中点,则三棱锥A-BEF的外接球的半径R=1,内切球半径r=2-$\sqrt{3}$.
如图,正三棱锥A-BCD的侧棱长为2,底面BCD的边长为2$\sqrt{2}$,E,分别为BC,BD的中点,则三棱锥A-BEF的外接球的半径R=1,内切球半径r=2-$\sqrt{3}$.