题目内容
函数f(x)=
+x(x∈[1,3])的值域为( )
| 1 |
| x+1 |
| A、(-∞,1)∪(1,+∞) | ||||
B、[
| ||||
C、(
| ||||
D、[
|
考点:函数的值域
专题:计算题,导数的综合应用
分析:先求导f′(x)=1-(
)2=
,从而由导数的正负确定函数的单调性,从而求函数的值域.
| 1 |
| x+1 |
| x(x+2) |
| (x+1)2 |
解答:
解:∵f′(x)=1-(
)2=
>0,(x∈[1,3])
∴f(x)在[1,3]上单调递增,
∴fmin(x)=f(1)=
,
fmax(x)=f(3)=
,
∴f(x)的值域为[
,
];
故选D.
| 1 |
| x+1 |
| x(x+2) |
| (x+1)2 |
∴f(x)在[1,3]上单调递增,
∴fmin(x)=f(1)=
| 3 |
| 2 |
fmax(x)=f(3)=
| 13 |
| 4 |
∴f(x)的值域为[
| 3 |
| 2 |
| 13 |
| 4 |
故选D.
点评:本题考查了导数的综合应用及函数的值域的求法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=lg(|x|+1)-sin2x的零点个数为( )
| A、9 | B、10 | C、11 | D、12 |
在平行四边形ABCD中,对角线AC与BD交于点O,若
+
=λ
,则实数λ等于( )
| AB |
| AD |
| AO |
| A、4 | B、3 | C、2 | D、1 |
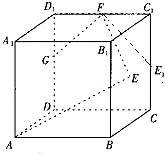 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E是正方形BCC1B1的中心,点F,G分别是棱C1D1,DD1的中点.设点E1是点E在平面DCC1D1内的正投影.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E是正方形BCC1B1的中心,点F,G分别是棱C1D1,DD1的中点.设点E1是点E在平面DCC1D1内的正投影.