题目内容
已知双曲线x2-y2=1,点A是它的左顶点,c是它的半焦距,点B(c2,0),点P是双曲线右支上的点,且满足AP⊥BP,求点P的坐标.
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:求出双曲线的a,b,c,可得A、B的坐标,设出P的坐标(m,n),由两直线垂直的条件结合斜率公式可得m,n的关系,联立m2-n2=1,即可解得m,n.
解答:
解:双曲线x2-y2=1的a=1,b=1,c=
,
则A(-1,0),B(2,0),设P(m,n)(m>0),
由AP⊥BP,即有kAPkBP=-1,
即
•
=-1,
即有n2=-(m+1)(m-2),
又m2-n2=1,即n2=m2-1,
由1-m2=(m+1)(m-2).
解得m=
(-1舍去),
即有n2=
-1,解得n=±
,
则点P的坐标为(
,
)或(
,-
).
| 2 |
则A(-1,0),B(2,0),设P(m,n)(m>0),
由AP⊥BP,即有kAPkBP=-1,
即
| n |
| m+1 |
| n |
| m-2 |
即有n2=-(m+1)(m-2),
又m2-n2=1,即n2=m2-1,
由1-m2=(m+1)(m-2).
解得m=
| 3 |
| 2 |
即有n2=
| 9 |
| 4 |
| ||
| 2 |
则点P的坐标为(
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| ||
| 2 |
点评:本题考查双曲线的方程和性质,同时考查两直线垂直的条件和斜率公式,运用点在曲线上满足曲线方程,联立方程求解是解题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
如图所示,程序框图算法流程图的输出结果s的值为( )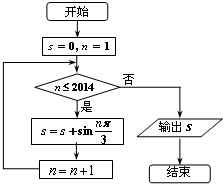

A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
函数f(x)=
+x(x∈[1,3])的值域为( )
| 1 |
| x+1 |
| A、(-∞,1)∪(1,+∞) | ||||
B、[
| ||||
C、(
| ||||
D、[
|
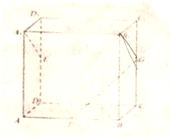 如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,E,F,G分别是DD1,AB,CC1的中点,则异面直线A1E与GF所成角为
如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,E,F,G分别是DD1,AB,CC1的中点,则异面直线A1E与GF所成角为