题目内容
在平行四边形ABCD中，对角线AC与BD交于点O，若
+
=λ
，则实数λ等于（ ）
| AB |
| AD |
| AO |
| A、4 | B、3 | C、2 | D、1 |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：利用向量的平行四边形法则、向量共线定理即可得出．
解答：
解：∵在平行四边形ABCD中，对角线AC与BD交于点O，
∴
+
=
=2
，
∵
+
=λ
，
∴λ=2．
故选：C．
∴
| AB |
| AD |
| AC |
| AO |
∵
| AB |
| AD |
| AO |
∴λ=2．
故选：C．
点评：本题考查了向量的平行四边形法则、向量共线定理，属于基础题．
练习册系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
相关题目
如图所示，程序框图算法流程图的输出结果s的值为（ ）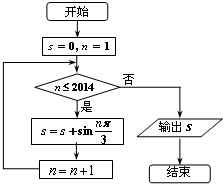
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
函数f（x）=
+x（x∈[1，3]）的值域为（ ）
| 1 |
| x+1 |
| A、（-∞，1）∪（1，+∞） | ||||
B、[
| ||||
C、（
| ||||
D、[
|
已知△ABC中，设角A，B，C所对的边分别为a，b，c，G为△ABC的重心，且a
+b
+c
=
，则△ABC为
（ ）
| GA |
| GB |
| GC |
| 0 |
（ ）
| A、等腰直角三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等边三角形 |
当a1，a2，…，a25是0或2时，形如x=
+
+…+
的一切数x，可满足（ ）
| a1 |
| 3 |
| a2 |
| 32 |
| a25 |
| 325 |
A、0≤x＜
| ||||
B、
| ||||
C、
| ||||
D、0≤x＜
|
如图，在平行四边形ABCD中，M为CD中点，若
=λ
+μ
．则μ的值为（ ）
| AC |
| AM |
| AB |
A、
| ||
B、
| ||
C、
| ||
| D、1 |