题目内容
函数f(x)=lg(|x|+1)-sin2x的零点个数为( )
| A、9 | B、10 | C、11 | D、12 |
考点:函数零点的判定定理
专题:计算题,作图题,函数的性质及应用
分析:函数f(x)=lg(|x|+1)-sin2x的零点个数即y=lg(|x|+1)与y=sin2x的图象的交点的个数,作图并利用三角函数的图象特征求解.
解答:
解:函数f(x)=lg(|x|+1)-sin2x的零点个数即
y=lg(|x|+1)与y=sin2x的图象的交点的个数,
作函数y=lg(|x|+1)与y=sin2x的图象如下,
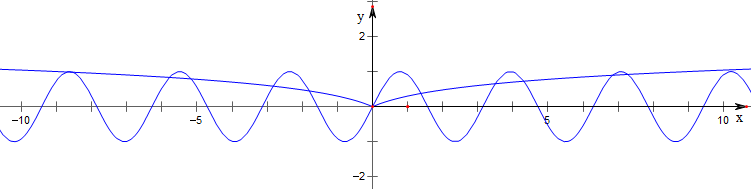
结合图象及三角函数的最值知,
图象在y轴左侧有6个交点,
在y轴右侧有5个交点,在y轴上有一个交点;
故选D.
y=lg(|x|+1)与y=sin2x的图象的交点的个数,
作函数y=lg(|x|+1)与y=sin2x的图象如下,

结合图象及三角函数的最值知,
图象在y轴左侧有6个交点,
在y轴右侧有5个交点,在y轴上有一个交点;
故选D.
点评:本题考查了函数的图象的应用及函数的零点的个数的判断,属于基础题.

练习册系列答案
相关题目
函数f(x)=
+x(x∈[1,3])的值域为( )
| 1 |
| x+1 |
| A、(-∞,1)∪(1,+∞) | ||||
B、[
| ||||
C、(
| ||||
D、[
|
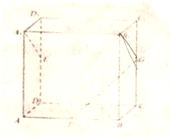 如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,E,F,G分别是DD1,AB,CC1的中点,则异面直线A1E与GF所成角为
如图,长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,E,F,G分别是DD1,AB,CC1的中点,则异面直线A1E与GF所成角为