题目内容
平面内动点M(x,y)与两定点A(-
,0),B(
,0)的连线的斜率之积为-
,记动点M的轨迹为C.
(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)定点F(-2,0),T为直线x=-3上任意一点,过F作TF的垂线交曲线C于点P,Q.
(i)证明:OT平分线段PQ(其中O为坐标原点);
(ii)当
最小时,求点T的坐标.
| 6 |
| 6 |
| 1 |
| 3 |
(Ⅰ)求动点M的轨迹C的方程;
(Ⅱ)定点F(-2,0),T为直线x=-3上任意一点,过F作TF的垂线交曲线C于点P,Q.
(i)证明:OT平分线段PQ(其中O为坐标原点);
(ii)当
| |TF| |
| |PQ| |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(I)由已知可得kMA•kMB=
•
=-
,化简即可得出动点M的轨迹C的方程;
(II)(i)证明:设T(-3,m),则直线TF的斜率kTF=-m.当m≠0时,直线PQ的斜率kPQ=
,直线PQ的方程为:x=my-2,当m=0时,也满足上述方程.
设P(x1,y1),Q(x2,y2),与椭圆的方程联立化为(3+m2)y2-4my-2=0,可得y1+y2,y1y2,x1+x2.即可得出PQ的中点N.只要证明直线ON的斜率kON=kOT即可.
(ii)由(i)可得|TF|=
.利用弦长公式可得|PQ|=
=
.可得
=
,再利用基本不等式的性质即可得出.
| y | ||
x+
|
| y | ||
x-
|
| 1 |
| 3 |
(II)(i)证明:设T(-3,m),则直线TF的斜率kTF=-m.当m≠0时,直线PQ的斜率kPQ=
| 1 |
| m |
设P(x1,y1),Q(x2,y2),与椭圆的方程联立化为(3+m2)y2-4my-2=0,可得y1+y2,y1y2,x1+x2.即可得出PQ的中点N.只要证明直线ON的斜率kON=kOT即可.
(ii)由(i)可得|TF|=
| m2+1 |
| (1+m2)[(y1+y2)2-4y1y2] |
| ||
| 3+m2 |
| |TF| |
| |PQ| |
|
解答:
解:(I)由已知可得kMA•kMB=
•
=-
,
化为
+
=1(y≠0),
∴动点M的轨迹C的方程为
+
=1(y≠0);
(II)(i)证明:设T(-3,m),则直线TF的斜率kTF=
=-m.
当m≠0时,直线PQ的斜率kPQ=
,直线PQ的方程为:x=my-2,
当m=0时,PQ的方程为:x=-2,也满足上述方程.
设P(x1,y1),Q(x2,y2),联立
,
化为(3+m2)y2-4my-2=0,
△=16m2+8(m2+3)>0,
∴y1+y2=
,y1y2=
,
∴x1+x2=m(y1+y2)-4=
.
∴PQ的中点N(
,
).
∴直线ON的斜率kON=-
.
又直线OT的斜率kOT=-
.
∴点N在直线OT上,
∴OT平分线段PQ.
(ii)由(i)可得|TF|=
.
|PQ|=
=
=
.
∴
=
=
≥
=
,当且仅当m=±1时取等号.
∴当
最小时,点T的坐标为(-3,±1).
| y | ||
x+
|
| y | ||
x-
|
| 1 |
| 3 |
化为
| x2 |
| 6 |
| y2 |
| 2 |
∴动点M的轨迹C的方程为
| x2 |
| 6 |
| y2 |
| 2 |
(II)(i)证明:设T(-3,m),则直线TF的斜率kTF=
| m-0 |
| -3-(-2) |
当m≠0时,直线PQ的斜率kPQ=
| 1 |
| m |
当m=0时,PQ的方程为:x=-2,也满足上述方程.
设P(x1,y1),Q(x2,y2),联立
|
化为(3+m2)y2-4my-2=0,
△=16m2+8(m2+3)>0,
∴y1+y2=
| 4m |
| 3+m2 |
| -2 |
| 3+m2 |
∴x1+x2=m(y1+y2)-4=
| -12 |
| m2+3 |
∴PQ的中点N(
| -6 |
| 3+m2 |
| 2m |
| 3+m2 |
∴直线ON的斜率kON=-
| m |
| 3 |
又直线OT的斜率kOT=-
| m |
| 3 |
∴点N在直线OT上,
∴OT平分线段PQ.
(ii)由(i)可得|TF|=
| m2+1 |
|PQ|=
| (1+m2)[(y1+y2)2-4y1y2] |
(1+m2)[(
|
| ||
| 3+m2 |
∴
| |TF| |
| |PQ| |
|
|
|
| ||
| 3 |
∴当
| |TF| |
| |PQ| |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、弦长公式、直线平分线段问题、斜率计算公式、基本不等式的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
设数列{an}为公差为2的等差数列,记{an}的前n项和为Sn,令bn=Sn+an,若{bn}为递增数列,则a1的取值范围是( )
| A、(-4,+∞) |
| B、(-3,+∞) |
| C、(-2,+∞) |
| D、(0,+∞) |
如图所示,程序框图算法流程图的输出结果s的值为( )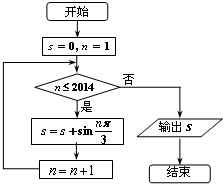

A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
函数f(x)=
+x(x∈[1,3])的值域为( )
| 1 |
| x+1 |
| A、(-∞,1)∪(1,+∞) | ||||
B、[
| ||||
C、(
| ||||
D、[
|