题目内容
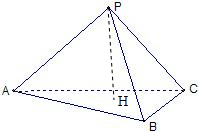 如图,在三棱锥P-ABC中,三个侧棱PA、PB、PC两两垂直,PH⊥底面ABC.求证:
如图,在三棱锥P-ABC中,三个侧棱PA、PB、PC两两垂直,PH⊥底面ABC.求证:(1)AH⊥BC;
(2)BH⊥AC;
(3)CH⊥AB.
考点:直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)(2)(3)的证明方法一样,以(1)为例,要证AH⊥BC,只需要证BC⊥平面PAH,要只需要证PH⊥BC,PA⊥BC,只需要证PA⊥平面PBC,根据已知条件可证.
解答:
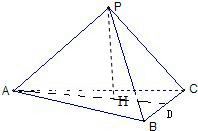 证明(1)如图所示,连接AH交BC于点D.
证明(1)如图所示,连接AH交BC于点D.
∵PA⊥PB,PA⊥PC,PB∩PC=C
∴PA⊥平面PBC,
又BC?平面PBC,
∴PA⊥BC
∵PH⊥底面ABC,BC?平面ABC
∴PH⊥BC,
又PA∩PH=P
∴BC⊥平面PAH,
∵AH?平面PAH,
∴BC⊥AH
(2)(3)同理可证
∴BH⊥AC;CH⊥AB.
 证明(1)如图所示,连接AH交BC于点D.
证明(1)如图所示,连接AH交BC于点D.∵PA⊥PB,PA⊥PC,PB∩PC=C
∴PA⊥平面PBC,
又BC?平面PBC,
∴PA⊥BC
∵PH⊥底面ABC,BC?平面ABC
∴PH⊥BC,
又PA∩PH=P
∴BC⊥平面PAH,
∵AH?平面PAH,
∴BC⊥AH
(2)(3)同理可证
∴BH⊥AC;CH⊥AB.
点评:本题主要考查了线线垂直和线面垂直的判定定理和性质,关键是之间的它们转化,属于中档题.

练习册系列答案
相关题目
若复数z满足z•(1+2i)=1,则
=( )
| z |
A、
| ||||
| B、1-2i | ||||
C、
| ||||
| D、1+2i |
若直线l不平行于平面 α,且l?α,则( )
| A、α内不存在与l平行的直线 |
| B、α内的所有直线与l异面 |
| C、α内存在唯一的直线与l平行 |
| D、α内的直线与l都相交 |
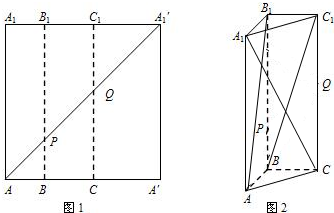 已知矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成图2所示的三棱柱ABC-A1B1C1,若面对角线AB1⊥BC1,求证:A1C⊥AB1.
已知矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成图2所示的三棱柱ABC-A1B1C1,若面对角线AB1⊥BC1,求证:A1C⊥AB1.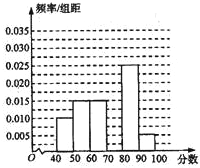 某校高一年级有2000名学生,从中随机抽出60名学生,将这60名学生的某次数学考试成绩(百分制)分成六段[40,50),[50,60),…,[90,100]后,得到如图所示的频率分布直方图,观察图形的信息,回答下列问题:
某校高一年级有2000名学生,从中随机抽出60名学生,将这60名学生的某次数学考试成绩(百分制)分成六段[40,50),[50,60),…,[90,100]后,得到如图所示的频率分布直方图,观察图形的信息,回答下列问题: