题目内容
判断下列命题是否正确，正确的说明理由，错误的举例说明：
（1）已知平面α、β和直线m、n，若m?α，n?β，m∥β，n∥β，则α∥β．
（2）一个平面α内两条不平行的直线都平行于另一平面β，则α∥β．
（1）已知平面α、β和直线m、n，若m?α，n?β，m∥β，n∥β，则α∥β．
（2）一个平面α内两条不平行的直线都平行于另一平面β，则α∥β．
考点：平面与平面平行的判定,空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：（1）举反例说明就可以，通过画图说明；
（2）利用反证法来证明．
（2）利用反证法来证明．
解答：
解：（1）错误，例如如图所示：m?α，n?β，m∥β，n∥α，α∩β=l．
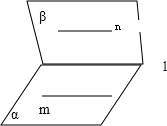
（2）用反证法来证明，假如这两个平面不平行，那它们相交于一条直线O，O如果与平面α中的a，b中的一条相交，
与另一条平行，则O也与平面β中的c，d一条相交，一条平行，而这两种都可以证明这两个平面式一个平面，与假设不符，
而如果O与平面α中的a，b都相交的话，那就也与平面B中的c，d都相交，这也是不可能的，
综上所述，α∥β．
（2）用反证法来证明，假如这两个平面不平行，那它们相交于一条直线O，O如果与平面α中的a，b中的一条相交，
与另一条平行，则O也与平面β中的c，d一条相交，一条平行，而这两种都可以证明这两个平面式一个平面，与假设不符，
而如果O与平面α中的a，b都相交的话，那就也与平面B中的c，d都相交，这也是不可能的，
综上所述，α∥β．
点评：本题主要考查了线面平行和面面平行的关系，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
已知函数f（x）定义域是R，满足对任意的x1＜x2，都有
＞0，且A（0，-2），B（3，2）是其图象上的两点，那么|f（x+1）|＜2的解集是（ ）
| f(x1)-f(x2) |
| x1-x2 |
| A、（1，4） |
| B、（-1，2） |
| C、（-∞，1）∪[4，+∞] |
| D、（-∞，-1）∪[2，+∞） |
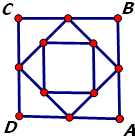正方形ABCD的边长为1，选各边的中点按如图连成正方形，再选各边中点连成正方形，依次无限做下去，则所有正方形的边长之和为（ ）
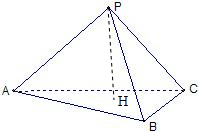如图，在三棱锥P-ABC中，三个侧棱PA、PB、PC两两垂直，PH⊥底面ABC．求证：
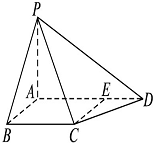如图，在四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB．