题目内容
设f(x)=x2-(k+1)x+k
(1)若关于x的不等式f(x)<0为(1,2),求实数k的值;
(2)设k>1且k≠2,求关于x的不等式
<0的解集.
(1)若关于x的不等式f(x)<0为(1,2),求实数k的值;
(2)设k>1且k≠2,求关于x的不等式
| f(x) |
| 2-x |
考点:其他不等式的解法,一元二次不等式的解法
专题:不等式的解法及应用
分析:(1)由题意可得 1和2是x2-(k+1)x+k=0的两个根,由韦达定理可得 k的值.
(2)设k>1且k≠2,关于x的不等式即
>0.
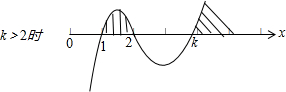
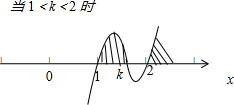
当k>2时,和 1<k<2两种情况,分别利用穿根法求得不等式的解集.
(2)设k>1且k≠2,关于x的不等式即
| (x-1)(x-k) |
| x-2 |
当k>2时,和 1<k<2两种情况,分别利用穿根法求得不等式的解集.
解答:
解:(1)∵f(x)=x2-(k+1)x+k,不等式f(x)<0为(1,2),
∴1和2是x2-(k+1)x+k=0的两个根,由韦达定理可得1×2=k,即 k=2.
(2)设k>1且k≠2,关于x的不等式
<0,即
<0,
即
>0.
当k>2时,利用穿根法求得不等式的解集为{x|1<x<2,或x>k};
当 1<k<2时,利用穿根法求得不等式的解集为{x|1<x<k,或x>2}.
∴1和2是x2-(k+1)x+k=0的两个根,由韦达定理可得1×2=k,即 k=2.
(2)设k>1且k≠2,关于x的不等式
| f(x) |
| 2-x |
| (x-1)(x-k) |
| 2-x |
即
| (x-1)(x-k) |
| x-2 |
当k>2时,利用穿根法求得不等式的解集为{x|1<x<2,或x>k};
当 1<k<2时,利用穿根法求得不等式的解集为{x|1<x<k,或x>2}.


点评:本题主要考查分式不等式、一元二次不等式的解法,体现了转化、分类讨论、数形结合的数学思想,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图所示的程序框图,运行相应的程序,若输入x的值为4,则输出y的值为( )


| A、2 | B、4 | C、8 | D、16 |
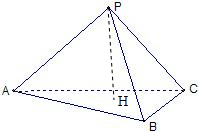 如图,在三棱锥P-ABC中,三个侧棱PA、PB、PC两两垂直,PH⊥底面ABC.求证:
如图,在三棱锥P-ABC中,三个侧棱PA、PB、PC两两垂直,PH⊥底面ABC.求证: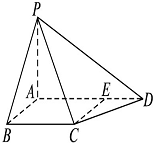 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB.