题目内容
已知偶函数f（x）在[0，+∞）上单调递减，f（2）=0，则满足不等式f（x）＞0的实数x的取值范围是 ．
考点：奇偶性与单调性的综合
专题：函数的性质及应用
分析：可以根据该函数在[0，+∞）上单调递减，f（2）=0，是偶函数，大体画出该函数图象的草图，结合图象可列出关于x的不等式．
解答：
解：∵偶函数f（x）在[0，+∞）上单调递减，且f（2）=0，
∴该函数在（-∞，0）上递增，且f（-2）=0，
∴可画出该函数的图象的草图如下：
可见，当-2＜x＜2时，f（x）＞0．
故答案为：（-2，2）．
∴该函数在（-∞，0）上递增，且f（-2）=0，
∴可画出该函数的图象的草图如下：
可见，当-2＜x＜2时，f（x）＞0．
故答案为：（-2，2）．
点评：抽象函数的问题常采用数形结合的方法解决问题，本题作为填空题，采用数形结合思想来解，既快捷，有准确．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
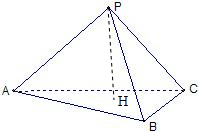如图，在三棱锥P-ABC中，三个侧棱PA、PB、PC两两垂直，PH⊥底面ABC．求证：