题目内容
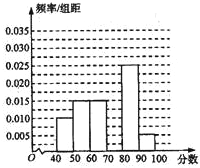 某校高一年级有2000名学生,从中随机抽出60名学生,将这60名学生的某次数学考试成绩(百分制)分成六段[40,50),[50,60),…,[90,100]后,得到如图所示的频率分布直方图,观察图形的信息,回答下列问题:
某校高一年级有2000名学生,从中随机抽出60名学生,将这60名学生的某次数学考试成绩(百分制)分成六段[40,50),[50,60),…,[90,100]后,得到如图所示的频率分布直方图,观察图形的信息,回答下列问题:(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)根据频率分布直方图推测,高一年级2000名学生在该次数学考试中成绩低于60分的人数;
(3)统计方法中,同一组数据常用该组区间的中点值作为代表,请根据频率分布直方图估计高一年级该次数学考试的平均成绩.
考点:频率分布直方图
专题:概率与统计
分析:(1)由频率分布直方图能求出分数在[70,80)内的频率,并由此能补全频率分布直方图.
(2)根据频率分布直方图能求出高一年级2000名学生在该次数学考试中成绩低于60分的人数.
(3)根据频率分布直方图能求出高一年级该次数学考试的平均成绩.
(2)根据频率分布直方图能求出高一年级2000名学生在该次数学考试中成绩低于60分的人数.
(3)根据频率分布直方图能求出高一年级该次数学考试的平均成绩.
解答:
解:(1)由频率分布直方图知分数在[70,80)内的频率为: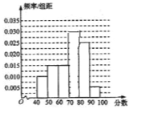
1-[(0.010+0.015+0.015+0.025+0.005)×10]=0.3.
这个频率分布直方图如右图.
(2)根据频率分布直方图推测,
高一年级2000名学生在该次数学考试中成绩低于60分的人数为:
2000×[(0.01+0.015)×10]=500(人).
(3)高一年级该次数学考试的平均成绩为:
45×0.1+55×0.15+65×0.15+75×0.3+80×0.25+95×0.05=69.75.

1-[(0.010+0.015+0.015+0.025+0.005)×10]=0.3.
这个频率分布直方图如右图.
(2)根据频率分布直方图推测,
高一年级2000名学生在该次数学考试中成绩低于60分的人数为:
2000×[(0.01+0.015)×10]=500(人).
(3)高一年级该次数学考试的平均成绩为:
45×0.1+55×0.15+65×0.15+75×0.3+80×0.25+95×0.05=69.75.
点评:本题考查频率分布直方图的应用,解题时要认真审题,是基础题.

练习册系列答案
相关题目
 阅读如图所示的程序框图.若输入m=8,n=6,则输出的a,i分别等于( )
阅读如图所示的程序框图.若输入m=8,n=6,则输出的a,i分别等于( )| A、12,2 | B、12,3 |
| C、24,2 | D、24,3 |
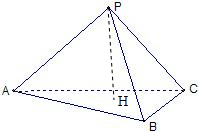 如图,在三棱锥P-ABC中,三个侧棱PA、PB、PC两两垂直,PH⊥底面ABC.求证:
如图,在三棱锥P-ABC中,三个侧棱PA、PB、PC两两垂直,PH⊥底面ABC.求证: