题目内容
已知二阶矩阵M满足:M
=
.
(Ⅰ)求矩阵M2;
(Ⅱ)求M2014
.
|
|
(Ⅰ)求矩阵M2;
(Ⅱ)求M2014
|
考点:矩阵与向量乘法的意义
专题:选作题,矩阵和变换
分析:(Ⅰ)根据所给的矩阵求这个矩阵的逆矩阵,可以首先求出ad-bc的值,再代入逆矩阵的公式,可求M,即可求出矩阵M2;
(Ⅱ)M2014
=M2
.即可求M2014
.
(Ⅱ)M2014
|
|
|
解答:
解:(Ⅰ)记矩阵A=
,故|A|=-1,故A-1=
.
由已知得M=
=
,
∴M2=
=
;
(Ⅱ)M2014
=M2
=
.
|
|
由已知得M=
|
|
|
∴M2=
|
|
|
(Ⅱ)M2014
|
|
|
点评:本题考查逆变换与逆矩阵,本题是一个基础题,解题的关键是记住求逆矩阵的公式,代入数据时,不要出错,属于基础题.

练习册系列答案
相关题目
点P(-1,1)关于直线ax-y+b=0的对称点是Q(3,-1),则a、b的值依次是( )
| A、-2,2 | ||||
| B、2,-2 | ||||
C、
| ||||
D、-
|
 阅读如图所示的程序框图.若输入m=8,n=6,则输出的a,i分别等于( )
阅读如图所示的程序框图.若输入m=8,n=6,则输出的a,i分别等于( )| A、12,2 | B、12,3 |
| C、24,2 | D、24,3 |
已知集合A={x|1<x<4},B={x|x2-2x-3≤0},则A∩B=( )
| A、(-1,3) |
| B、(1,3] |
| C、[3,4) |
| D、[-1,4) |
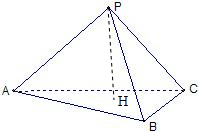 如图,在三棱锥P-ABC中,三个侧棱PA、PB、PC两两垂直,PH⊥底面ABC.求证:
如图,在三棱锥P-ABC中,三个侧棱PA、PB、PC两两垂直,PH⊥底面ABC.求证: