题目内容
若复数z满足z•（1+2i）=1，则
=（ ）
| z |
A、
| ||||
| B、1-2i | ||||
C、
| ||||
| D、1+2i |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：利用复数的运算法则、共轭复数的定义即可得出．
解答：
解：∵复数z满足z•（1+2i）=1，∴z（1+2i）（1-2i）=1-2i，∴z=
-
i．
∴
=
+
i．
故选：C．
| 1 |
| 5 |
| 2 |
| 5 |
∴
. |
| z |
| 1 |
| 5 |
| 2 |
| 5 |
故选：C．
点评：本题考查了复数的运算法则、共轭复数的定义，属于基础题．
练习册系列答案
相关题目
12个篮球队中有3个强队，任意分成三个组（每组4个队），则3个强队恰好被分在同一组的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
下列关于函数f（x）=sin（2x+
）的结论：
①f（x）的最小正周期是2π；
②f（x）在区间[kπ-
，kπ+
]（k∈Z）上单调递增；
③当x∈[0，
]时，f（x）的值域为[-
，
]；
④函数y=f（x+
）是偶函数．
其中正确的结论为（ ）
| π |
| 3 |
①f（x）的最小正周期是2π；
②f（x）在区间[kπ-
| 5π |
| 12 |
| π |
| 12 |
③当x∈[0，
| π |
| 2 |
| ||
| 2 |
| ||
| 2 |
④函数y=f（x+
| π |
| 12 |
其中正确的结论为（ ）
| A、①② | B、②③ | C、②④ | D、③④ |
点P（-1，1）关于直线ax-y+b=0的对称点是Q（3，-1），则a、b的值依次是（ ）
| A、-2，2 | ||||
| B、2，-2 | ||||
C、
| ||||
D、-
|
已知函数f（x）定义域是R，满足对任意的x1＜x2，都有
＞0，且A（0，-2），B（3，2）是其图象上的两点，那么|f（x+1）|＜2的解集是（ ）
| f(x1)-f(x2) |
| x1-x2 |
| A、（1，4） |
| B、（-1，2） |
| C、（-∞，1）∪[4，+∞] |
| D、（-∞，-1）∪[2，+∞） |
已知奇函数f（x）满足对于?x∈R，都有f（1+x）=f（1-x），且当x∈[-1，0]时，f（x）=-x2，又函数g（x）=|sinπx|，则函数h（x）=f（x）-g（x）在[-2，2]上的零点个数是（ ）
| A、4 | B、5 | C、6 | D、7 |
如图所示的程序框图，运行相应的程序，若输入x的值为4，则输出y的值为（ ）
| A、2 | B、4 | C、8 | D、16 |
阅读如图所示的程序框图．若输入m=8，n=6，则输出的a，i分别等于（ ）| A、12，2 | B、12，3 |
| C、24，2 | D、24，3 |
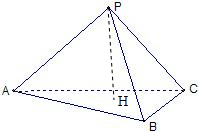如图，在三棱锥P-ABC中，三个侧棱PA、PB、PC两两垂直，PH⊥底面ABC．求证：