题目内容
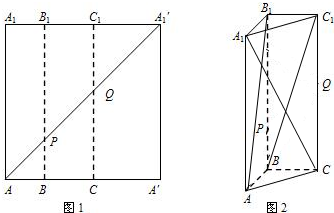 已知矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成图2所示的三棱柱ABC-A1B1C1,若面对角线AB1⊥BC1,求证:A1C⊥AB1.
已知矩形纸片AA′A1′A1,点B、C、B1、C1分别为AA′、A1A1′的三等分点,将矩形纸片沿BB1、CC1折成图2所示的三棱柱ABC-A1B1C1,若面对角线AB1⊥BC1,求证:A1C⊥AB1.考点:直线与平面垂直的性质
专题:空间位置关系与距离
分析:延长B1C1到D,使DC1=B1C1,根据三角形外接圆的性质证明出A1D⊥A1B1,进而根据线面垂直的性质推断出AA1⊥A1D,进而证明出A1D⊥平面AA1B1,推断出AB1⊥A1D,根据四边形BCC1D为平行四边形,推断出BC1∥CD,进而依据AB1⊥BC1,证明出AB1⊥CD,然后根据线面垂直的判定定理证明出AB1⊥平面CA1D,最后利用线面垂直的性质证明出A1C⊥AB1.
解答:
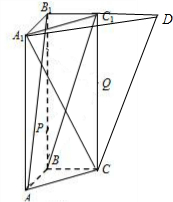 证明:延长B1C1到D,使DC1=B1C1,
证明:延长B1C1到D,使DC1=B1C1,
依题意知B1C1=A1C1=DC1,
∴∠B1A1D=90°,即A1D⊥A1B1,
∵AA1⊥平面A1B1C1,A1D?平面A1B1C1,
∴AA1⊥A1D,
∵A1B1?平面AA1B1,AA1?平面AA1B1,A1B1∩AA1=A1,
∴A1D⊥平面AA1B1,
∵AB1?平面AA1B1,
∴AB1⊥A1D,
∵BC∥C1D,BC=C1D,
∴四边形BCC1D为平行四边形,
∴BC1∥CD,
∵AB1⊥BC1,
∴AB1⊥CD,
∵CD?平面CA1D,A1D?平面CA1D,A1D∩CD=D,
∴AB1⊥平面CA1D,
∵A1C?平面CA1D,
∴AB1⊥A1C.
 证明:延长B1C1到D,使DC1=B1C1,
证明:延长B1C1到D,使DC1=B1C1,依题意知B1C1=A1C1=DC1,
∴∠B1A1D=90°,即A1D⊥A1B1,
∵AA1⊥平面A1B1C1,A1D?平面A1B1C1,
∴AA1⊥A1D,
∵A1B1?平面AA1B1,AA1?平面AA1B1,A1B1∩AA1=A1,
∴A1D⊥平面AA1B1,
∵AB1?平面AA1B1,
∴AB1⊥A1D,
∵BC∥C1D,BC=C1D,
∴四边形BCC1D为平行四边形,
∴BC1∥CD,
∵AB1⊥BC1,
∴AB1⊥CD,
∵CD?平面CA1D,A1D?平面CA1D,A1D∩CD=D,
∴AB1⊥平面CA1D,
∵A1C?平面CA1D,
∴AB1⊥A1C.
点评:本题主要考查了线面垂直的性质和判定定理的运用.作出平面CA1D,并证明出AB1⊥平面CA1D是关键.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
已知奇函数f(x)满足对于?x∈R,都有f(1+x)=f(1-x),且当x∈[-1,0]时,f(x)=-x2,又函数g(x)=|sinπx|,则函数h(x)=f(x)-g(x)在[-2,2]上的零点个数是( )
| A、4 | B、5 | C、6 | D、7 |
已知集合A={x|1<x<4},B={x|x2-2x-3≤0},则A∩B=( )
| A、(-1,3) |
| B、(1,3] |
| C、[3,4) |
| D、[-1,4) |
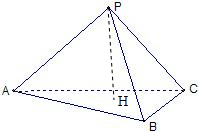 如图,在三棱锥P-ABC中,三个侧棱PA、PB、PC两两垂直,PH⊥底面ABC.求证:
如图,在三棱锥P-ABC中,三个侧棱PA、PB、PC两两垂直,PH⊥底面ABC.求证: