题目内容
若直线l不平行于平面 α,且l?α,则( )
| A、α内不存在与l平行的直线 |
| B、α内的所有直线与l异面 |
| C、α内存在唯一的直线与l平行 |
| D、α内的直线与l都相交 |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:根据线面关系的定义,直线l不平行于平面α,且l?α,判断出直线l与α的关系,利用直线与平面相交的定义,即可得到结论.
解答:
解:直线l不平行于平面α,且l?α,
则l与α相交
l与α内的直线可能相交,也可能异面,但不可能平行
故B,C,D错误
故选:A.
则l与α相交
l与α内的直线可能相交,也可能异面,但不可能平行
故B,C,D错误
故选:A.
点评:本题考查线线、线面位置关系的判定,考查逻辑推理能力和空间想象能力.其中利用已知判断出直线l与α的关系是解答本题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
下列关于函数f(x)=sin(2x+
)的结论:
①f(x)的最小正周期是2π;
②f(x)在区间[kπ-
,kπ+
](k∈Z)上单调递增;
③当x∈[0,
]时,f(x)的值域为[-
,
];
④函数y=f(x+
)是偶函数.
其中正确的结论为( )
| π |
| 3 |
①f(x)的最小正周期是2π;
②f(x)在区间[kπ-
| 5π |
| 12 |
| π |
| 12 |
③当x∈[0,
| π |
| 2 |
| ||
| 2 |
| ||
| 2 |
④函数y=f(x+
| π |
| 12 |
其中正确的结论为( )
| A、①② | B、②③ | C、②④ | D、③④ |
如图所示的程序框图,运行相应的程序,若输入x的值为4,则输出y的值为( )


| A、2 | B、4 | C、8 | D、16 |
 阅读如图所示的程序框图.若输入m=8,n=6,则输出的a,i分别等于( )
阅读如图所示的程序框图.若输入m=8,n=6,则输出的a,i分别等于( )| A、12,2 | B、12,3 |
| C、24,2 | D、24,3 |
已知集合A={x|1<x<4},B={x|x2-2x-3≤0},则A∩B=( )
| A、(-1,3) |
| B、(1,3] |
| C、[3,4) |
| D、[-1,4) |
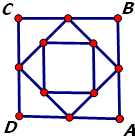 正方形ABCD的边长为1,选各边的中点按如图连成正方形,再选各边中点连成正方形,依次无限做下去,则所有正方形的边长之和为( )
正方形ABCD的边长为1,选各边的中点按如图连成正方形,再选各边中点连成正方形,依次无限做下去,则所有正方形的边长之和为( )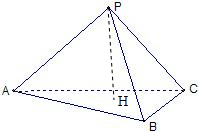 如图,在三棱锥P-ABC中,三个侧棱PA、PB、PC两两垂直,PH⊥底面ABC.求证:
如图,在三棱锥P-ABC中,三个侧棱PA、PB、PC两两垂直,PH⊥底面ABC.求证: